Varianzanalyse

Die Varianzanalyse ist ein statistisches Verfahren, das den Einfluss einer oder mehrerer nominal‐ oder ordinalskalierter unabhängiger Variablen auf eine oder mehrere metrische, abhängige Variablen untersucht.

Die unabhängige Variable wird als Faktor, Treatmentfaktor oder einfach nur als Treatment bezeichnet. Deren Ausprägungen heißen Faktorstufen. Eine Varianzanalyse wird immer dann durchgeführt, wenn es mehr als zwei Faktorstufen gibt.

Bei zwei Faktorstufen wird der t-Test gerechnet. Der t-Test wäre bei mehr als zwei Faktorstufen einerseits aufwendiger, andererseits kommt es durch die Sequenzierung von t-Tests zu einer 𝛼-Fehler Kumulierung und die Teststärke sinkt.

Es werden nach der Anzahl der Faktoren und abhängigen Variablen vier Formen der Varianzanalyse unterschieden:

• Bei nur einem Faktor und einer abhängigen Variable spricht man von der univariaten einfaktoriellen Varianzanalyse oder einer einfaktoriellen ANOVA (=Analysis of Variance).
• Bei mehreren Faktoren und einer abhängigen Variable spricht man von der univariaten mehrfaktoriellen Varianzanalyse oder einer mehrfaktoriellen ANOVA.
• Bei nur einem Faktor und mehreren abhängigen Variablen spricht man von der multivariaten einfaktoriellen Varianzanalyse oder einer einfaktoriellen MANOVA (=Multivariate Analysis of Variance).
• Bei mehreren Faktoren und mehreren abhängigen Variablen spricht man von der multivariaten mehrfaktoriellen Varianzanalyse oder einer mehrfaktoriellen MANOVA.

Voraussetzungen für die Varianzanalyse

• Die Fehlerkomponenten entstammen normalverteilten Grundgesamtheiten. Dafür ist nach dem zentralen Grenzwertsatz ein Stichprobenumfang von jeweils größer 30 hinreichend.
• Die Messwerte sind in allen Bedingungen voneinander unabhängig.
• Die abhängigen Variablen sind (quasi-)metrisch skaliert.
• Die Varianzen der Populationen der untersuchten Faktorstufen müssen gleich sein. Die Varianzhomogenität wird mit dem Levene-Test ermittelt. Ist der Test signifikant (d.h. p < ,05), unterscheiden sich die Varianzen der Stichproben und es muss eine Korrektur der Freiheitsgrade vorgenommen werden. Bei Verletzung dieser Varianzhomogenität kann der Welch-Test gerechnet werden.

Univariate einfaktorielle Varianzanalyse (ANOVA)

Eine einfaktorielle ANOVA ist ein statistisches Verfahren, das darauf abzielt zu untersuchen, ob es signifikante Unterschiede zwischen den Mittelwerten mehrerer Gruppen gibt. Dieses Verfahren ist besonders nützlich, wenn wir wissen möchten, ob verschiedene Treatments (oder auch Faktorstufen) einen erkennbaren, signifikanten Effekt auf eine uns interessierende abhängige Variable haben.

Statistisch prüft eine einfaktorielle ANOVA, ob signifikante Unterschiede zwischen den Mittelwerten dieser drei oder mehr Gruppen bestehen, was auf Unterschiede in den zugrunde liegenden Populationen hindeuten könnte, aus denen die Stichproben gezogen wurden. Genauer gesagt testet die ANOVA die Nullhypothese (H₀), dass alle Gruppenmittelwerte gleich sind (μ₁ = μ₂ = … = μ_k für k Gruppen), gegen die Alternativhypothese (H₁), dass mindestens zwei Gruppenmittelwerte signifikant unterschiedlich sind. Eine einfaktorielle ANOVA macht also eine Aussage über die Wahrscheinlichkeit, mit der die beobachteten (oder größere) Unterschiede zwischen den Stichprobenmittelwerten auftreten können, wenn die Nullhypothese wahr ist, dass alle Gruppenmittelwerte gleich sind.

Herzstück der ANOVA ist ein Vergleich: Wir vergleichen die Variabilität zwischen drei oder mehr Gruppen mit der Variabilität innerhalb dieser Gruppen. Die Variabilität zwischen den Gruppen gibt uns Aufschluss darüber, wie stark sich die Gruppenmittelwerte voneinander unterscheiden, während die Variabilität innerhalb der Gruppen die natürliche Streuung der Daten innerhalb jeder Gruppe widerspiegelt. Für diesen Vergleich nutzt die ANOVA das statistische Grundprinzip der Varianzzerlegung, das in Kontext der ANOVA spezifischer als Quadratsummenzerlegung bezeichnet wird. Dabei wird eine systematische Varianz („Varianz zwischen den Faktorstufen“) von der sogenannten Residualvarianz („Varianz innerhalb der Faktorstufen“) unterschieden.

Die systematische Varianz entsteht durch den Einfluss des Faktors bzw. der Gruppeneinteilung und wird deswegen auch als Varianz zwischen den Gruppen oder kurz als Zwischengruppenvarianz bezeichnet. Die Residualvarianz wird durch die Varianz innerhalb der Gruppen verursacht und umschreibt alle übrig gebliebene, zufällige Varianz, die nicht durch den Faktor bzw. die Gruppeneinteilung erklärt werden kann. Sie wird deswegen auch als Varianz innerhalb der Gruppen oder kurz als Innengruppenvarianz bezeichnet oder in anderen Kontexten auch als Fehler, Error, Rest, oder unaufgeklärte Varianz bezeichnet.

Terminologie

• Y : abhängige Variable
• X : Faktor
• k : Anzahl der Faktorstufen
• j : Kennzeichnung der Faktorstufe ( j = 1, 2, 3, … , k)
• i : Beobachtung innerhalb einer Faktorstufe
• N : Gesamtzahl der Beobachtungen
• n_j : Anzahl der Beobachtungen der j−ten Faktorstufe
• y_ij : i-te Beobachtung von Y in der j-ten Faktorstufe
• SY_j : Summe der beobachteten Werte unter der j-ten Faktorstufe
• ȳ_j : arithmetisches Mittel aller Messwerte unter der j-ten Faktorstufe
• SY : Gesamtsumme aller Messwerte für Y
• ȳ : arithmetisches Mittel aller Messwerte für Y

Signifikanztest der einfaktoriellen ANOVA

Um zu prüfen, ob sich die Mittelwerte der Gruppen mit hinreichender Sicherheit voneinander unterscheiden, wird der Signifikanztest der einfaktoriellen ANOVA gerechnet.

Zweiseitiges Problem

H_{0}: \mu_{1}=\mu_{2}=…=\mu_{k}

H_{1}:\neg H_{0} \qquad (mindestens\ ein\ Unterschied \ bei \ den\ Mittelwerten)

Quadratsummenzerlegung

Um den Signifikanztest der einfaktoriellen ANOVA zu berechnen, muss eine Varianzzerlegung durchgeführt werden, die als Quadratsummenzerlegung bezeichnet wird. Eine Quadratsumme ist ein statistischer Begriff, der die Summe der quadrierten Abweichungen aller beobachteten Werte von ihrem Mittelwert beschreibt. Größere Werte der Quadratsumme weisen auf eine größere Variabilität oder Streuung hin.

Die Quadratsummenzerlegung hat zum Ziel, die Gesamtvariabilität der Daten in zwei Teile zu zerlegen: die Variabilität zwischen den Gruppen und die Variabilität innerhalb der Gruppen. Die Gesamtquadratsumme QS_tot ist gleich der Summe der Quadratsummen zwischen den Gruppen QS_X (auch SSB oder Treatmentquadratsumme genannt) plus der Quadratsummen innerhalb der Gruppen QS_e (auch SSW oder Fehlerquadratsumme):

QS_{tot}=QS_{X}+QS_{e}\qquad mit\qquad df_{tot}=df_{X}+df_{e}

Die Totale- oder Gesamtquadratsumme misst die gesamte Variabilität in den Daten und wird berechnet, indem man die quadrierten Abweichungen jedes einzelnen Beobachtungswertes vom Gesamtmittelwert aller Beobachtungen summiert. Der Gesamtmittelwert ist der Durchschnittswert aller Beobachtungen über alle Gruppen hinweg:

QS_{tot}=\sum_j\sum_i (y_{ij}-\bar{y})^2\qquad mit\qquad df_{tot}=N-1

Die Quadratsumme zwischen den Gruppen misst, wie viel die Gruppenmittelwerte voneinander abweichen. Dies wird berechnet, indem man für jede Gruppe die Differenz zwischen dem Gruppenmittelwert und dem Gesamtmittelwert quadriert, dies mit der Anzahl der Beobachtungen in der Gruppe multipliziert und dann diese Werte für alle Gruppen summiert:

QS_{X}=\sum_j n_j (\bar{y}_{j}-\bar{y})^2\qquad mit\qquad df_{X}=k-1

Die Quadratsumme innerhalb der Gruppen misst die Variabilität der Beobachtungen innerhalb jeder Gruppe, also wie weit die einzelnen Beobachtungen in einer Gruppe vom Gruppenmittelwert entfernt sind. Sie wird berechnet, indem man die quadrierten Abweichungen jedes Beobachtungswertes vom Mittelwert seiner Gruppe summiert und dies über alle Gruppen hinweg tut:

QS_{e}=\sum_j\sum_i (y_{ij}-\bar{y}_{j})^2\qquad mit\qquad df_{e}=N-k

Vereinfachte Berechnung der Quadratsummenzerlegung

Bei einer einfaktoriellen ANOVA mit gleichen Stichprobengrößen, also wenn jede Gruppe dieselbe Anzahl von Beobachtungen (n) hat, kann die Berechnung der Quadratsummen etwas vereinfacht werden:

QS_{tot}=(2)-(1)\qquad mit\qquad df_{tot}=N-1

QS_{X}=(3)-(1)\qquad mit\qquad df_{X}=k-1

QS_{e}=(2)-(3)\qquad mit\qquad df_{e}=N-1

Dabei ist:

(1)=\frac{{SY}^2}{N}

(2)=\sum_j\sum_iy_{ij}^2

(3)=\sum_j(\frac{{SY}_j^2}{n})

Nur bei gleichen Stichprobengrößen (balanciertes Design) kann nämlich vereinfacht werden:

(3)=\frac{\sum_j{SY}_j^2}{n}

Signifikanztest (F-Test)

Die Prüfgröße F (F-Verteilung) wird berechnet, indem man das mittlere Quadrat zwischen den Gruppen durch das mittlere Quadrat innerhalb der Gruppen teilt.

Mittleres Quadrat (MQ) zwischen den Gruppen:

Um das mittlere Quadrat zwischen den Gruppen zu berechnen, teilt man die Quadratsumme zwischen den Gruppen QS_X durch die entsprechenden Freiheitsgrade df_X. Die Freiheitsgrade für das mittlere Quadrat zwischen den Gruppen entsprechen der Anzahl der Gruppen minus eins (k-1), wobei k die Anzahl der Gruppen ist:

MQ_{X}=\frac{QS_{X}}{df_X}

Sowie mittleres Quadrat innerhalb der Gruppen:

Um das mittlere Quadrat innerhalb der Gruppen zu berechnen, teilt man die Quadratsumme innerhalb der Gruppen QS_e durch die entsprechenden Freiheitsgrade df_e. Die Freiheitsgrade für das mittlere Quadrat innerhalb der Gruppen entsprechen der Gesamtanzahl der Beobachtungen minus der Anzahl der Gruppen (N-k), wobei N die Gesamtanzahl aller Beobachtungen ist:

MQ_{e}=\frac{QS_{e}}{df_e}

Die Prüfgröße F wird schließlich berechnet als:

F=\frac{MQ_{X}}{MQ_{e}}

Um die Signifikanz dieser Statistik zu beurteilen, wird die F-Verteilung verwendet. Ein hoher F-Wert deutet darauf hin, dass die Unterschiede zwischen den Gruppenmitteln größer sind, als man es aufgrund der zufälligen Variation innerhalb der Gruppen erwarten würde, was uns die Nullhypothese (dass alle Gruppenmittelwerte gleich sind) ablehnen lässt.

Testentscheidung nach festgelegtem Signifikanzniveau

• Der kritische Wert F_krit kann aus der F-Verteilungstabelle ausgelesen werden (unter Berücksichtigung des Signifikanzniveaus 𝛼 und der Freiheitsgrade df_X für die Spalten und df_e für die Zeilen). Fehlt der Eintrag für den Wert in der F-Verteilungstabelle, wird konservativ mit den nächstkleineren Freiheitsgraden gerechnet.
• H₀ wird abgelehnt, wenn F > F_krit.

Effektstärke η²

Die Effektstärke gibt an, wie stark der Effekt des Faktors auf die abhängige Variable ist. Nur wenn der F-Test signifikant ist, findet eine Berechnung der Effektstärke statt. Die Varianzaufklärung η² (sprich: Eta Quadrat) gibt an, welcher Anteil der Varianz, der abhängigen Variable, auf die Varianz, des Faktors, zurückgeführt werden kann.

η² wird berechnet, indem man die Quadratsumme zwischen den Gruppen QS_X durch die Gesamtquadratsumme QS_tot teilt:

\eta^2=\frac{QS_X}{QS_{tot}}=\frac{QS_X}{QS_X+QS_e}

Eta-Quadrat wird im Forschungsbericht in Prozent angegeben.

Post hoc-Verfahren

Der F-Test ist ein globaler Test. Ein signifikantes Testergebnis belegt Unterschiede zwischen mindestens zwei Faktorstufen, es bleibt jedoch unklar, welche Faktorstufen sich signifikant von anderen Faktorstufen unterscheiden. Um das aufzudecken werden sogenannte Post hoc-Tests durchgeführt.

Wenn davon ausgegangen werden kann, dass die Varianzen in der Population ähnlich sind, können sich folgende Post hoc-Tests je nach Einzelfall anbieten:

• Die Bonferroni-Korrektur liefert die beste Kontrolle über den α-Fehler.
• Der REGWQ / Tukey’s Test (Tukey HSD) weist eine gute Teststärke und strenge Kontrolle über den α-Fehler auf. Tukey ist eine sehr sichere Wahl, mit der man selten etwas falsch machen kann.
• Der Gabriel-Test wird bei leicht abweichenden Stichprobengrößen gerechnet.
• GT2 nach Hochberg wird bei stark abweichenden Stichprobengrößen verwendet.
• Dunnett wird gerechnet, wenn die Faktorstufen gegen einen Kontroll-Mittelwert verglichen werden sollen.

Wenn es Zweifel an der Ähnlichkeit der Varianzen gibt, wird Games-Howell gerechnet, dieser liefert allgemein die besten Ergebnisse und sollte immer berechnet werden.

Einfaktorielle ANOVA in R

Die Funktion unianova() aus dem tidycomm-Package berechnet einfaktorielle ANOVAs. Die unianova()-Funktion gibt, in einer Tabelle den kritischen Wert F_krit, die Freiheitsgrade der Treatmentquadratsumme df_num (Numerator: Zähler der F-Verteilung, Spalten in der Tabelle) und die Freiheitsgrade der Fehlerquadratsumme df_denom (Denominator: Nenner F-Verteilung, Zeilen in der Tabelle) an. Es wird der Name der abhängigen Variable und der p-Wert ausgegeben. Zusätzlich wird standartmäßig für die Effektstärke der Varianzaufklärung η² ausgegeben und der Levene-Test berechnet. Ist der Levene-Test signifikant liegt keine Varianzhomogenität vor. Die unianova()-Funktion rechnet dann automatisch den Welch-Test, der robust gegenüber Heteroskedastizität ist und es wird für die Effektstärke das konservativere Omega-Quadrat statt der Varianzaufklärung η² ausgegeben.

Mit dem WoJ-Datensatz und der unianova()-Funktion kann überprüft werden, ob aufgrund des aktuellen Beschäftigungsverhältnisses Journalist:innen mit hinreichender Sicherheit eine unterschiedliche Autonomie bei der Betonung, welche Aspekte einer Geschichte hervorgehoben werden (autonomy_emphasis), wahrnehmen.

Zunächst wird mit der describe()-Funktion aus dem tidycomm-Package und der group_by-Funktion aus dem dplyr-Package ermittelt, ob alle Voraussetzungen erfüllt sind.

Befehl:

WoJ %>%
  dplyr::group_by(employment) %>%
  describe(autonomy_emphasis)

Ausgabe:

# A tibble: 3 × 16
# Groups:   employment [3]
  employment Variable              N Missing     M    SD   Min   Q25   Mdn   Q75   Max Range CI_95_LL CI_95_UL Skewness Kurtosis
* <chr>      <chr>             <int>   <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
1 Freelancer autonomy_emphasis   171       1  3.90 0.852     1     4     4     4     5     4     3.77     4.03   -0.956     4.38
2 Full-time  autonomy_emphasis   898       4  4.12 0.781     1     4     4     5     5     4     4.07     4.17   -0.827     3.91
3 Part-time  autonomy_emphasis   126       0  4.02 0.759     1     4     4     4     5     4     3.88     4.15   -1.35      7.12

Die Voraussetzungen für einen F-Test sind gegeben, nachdem alle Teilstichproben größer 30 sind, darf nach dem zentralen Grenzwertsatz eine Normalverteilung der Fehlerkomponenten angenommen werden. Die Fehlerkomponenten sind voneinander unabhängig. Die abhängige Variable Autonomie bei der Entscheidung, welche Aspekte einer Geschichte hervorgehoben werden (autonomy_emphasis) ist quasimetrisch angegeben (1: „no freedom at all“ bis 5: „complete freedom“). Der Faktor Beschäftigungsverhätnis (employment) liegt dreistufig vor (Freelancer, Full-Time und Part-Time). Der Levene-Test ist nicht signifikant, es muss keine Korrektur der Freiheitsgrade vorgenommen werden. Somit darf der F-Test für einfaktorielle ANOVAs gerechnet werden.

Befehl:

WoJ %>% unianova(employment, autonomy_emphasis)

Ausgabe:

# A tibble: 1 × 8
  Variable                  F df_num df_denom         p eta_squared Levene_p var_equal
* <chr>             <num:.3!>  <dbl>    <dbl> <num:.3!>   <num:.3!>    <dbl> <chr>    
1 autonomy_emphasis     5.861      2     1192     0.003       0.010    0.175 TRUE 

Es können weitere abhängige Variablen ergänzt werden.

Befehl:

WoJ %>% unianova(employment, autonomy_emphasis, autonomy_selection)

Ausgabe:

The significant result from Levene's test suggests unequal variances among the groups, violating standard ANOVA assumptions. This necessitates the use of Welch's ANOVA, which is robust against heteroscedasticity.
# A tibble: 2 × 9
  Variable                   F df_num df_denom         p eta_squared omega_squared Levene_p var_equal
* <chr>              <num:.3!>  <dbl>    <dbl> <num:.3!>   <num:.3!>     <num:.3!>    <dbl> <chr>    
1 autonomy_emphasis      5.861      2     1192     0.003       0.010        NA        0.175 TRUE     
2 autonomy_selection     2.012      2      251     0.136      NA             0.002    0     FALSE   

Wenn keine abhängigen Variablen angegeben sind, werden alle (quasi-)metrischen Variablen verwendet.

Befehl:

WoJ %>% unianova(employment)

Ausgabe:

# A tibble: 11 × 9
   Variable                   F df_num df_denom         p omega_squared eta_squared Levene_p var_equal
 * <chr>              <num:.3!>  <dbl>    <dbl> <num:.3!>     <num:.3!>   <num:.3!>    <dbl> <chr>    
 1 autonomy_selection     2.012      2      251     0.136         0.002      NA        0     FALSE    
 2 autonomy_emphasis      5.861      2     1192     0.003        NA           0.010    0.175 TRUE     
 3 ethics_1               2.171      2     1197     0.115        NA           0.004    0.093 TRUE     
 4 ethics_2               2.204      2     1197     0.111        NA           0.004    0.802 TRUE     
 5 ethics_3               5.823      2      253     0.003         0.007      NA        0.001 FALSE    
 6 ethics_4               3.453      2     1197     0.032        NA           0.006    0.059 TRUE     
 7 work_experience        3.739      2      240     0.025         0.006      NA        0.034 FALSE    
 8 trust_parliament       1.527      2     1197     0.218        NA           0.003    0.103 TRUE     
 9 trust_government      12.864      2     1197     0.000        NA           0.021    0.083 TRUE     
10 trust_parties          0.842      2     1197     0.431        NA           0.001    0.64  TRUE     
11 trust_politicians      0.328      2     1197     0.721        NA           0.001    0.58  TRUE

Es ist über das optionale Argument descriptives auch möglich eine deskriptive Statistik mitausgeben zu lassen (Mittelwerte und Standartabweichungen der Faktorstufen).

Befehl:

WoJ %>% unianova(employment, autonomy_emphasis, descriptives = TRUE)

Ausgabe:

# A tibble: 1 × 14
  Variable                  F df_num df_denom         p eta_squared `M_Full-time` `SD_Full-time` `M_Part-time` `SD_Part-time` M_Freelancer SD_Freelancer Levene_p var_equal
* <chr>             <num:.3!>  <dbl>    <dbl> <num:.3!>   <num:.3!>         <dbl>          <dbl>         <dbl>          <dbl>        <dbl>         <dbl>    <dbl> <chr>    
1 autonomy_emphasis     5.861      2     1192     0.003       0.010          4.12          0.781          4.02          0.759         3.90         0.852    0.175 TRUE 

Es ist über das optionale Argument post_hoc auch möglich Post hoc-Verfahren anzuwenden. Standardmäßig wird Tukey’s HSD gerechnet, sind die Varianzen zu verschieden, wird automatisch Games-Howell angewendet.

Um das Ergebnis zu inspizieren, empfiehlt es sich die Analyse in einem separaten Modell zu speichern und dann auszuwerten:

Befehl:

model2<- WoJ %>% unianova(employment, autonomy_emphasis, post_hoc = TRUE)
View(model2)

Ausgabe:

Um das Ergebnis des Post hoc-Verfahrens zu sehen, muss mit der Maus die kleine Tabelle in der Zelle unter post_hoc-Zelle angewählt werden, dann öffnet sich eine neue Tabelle:

Ausgabe:

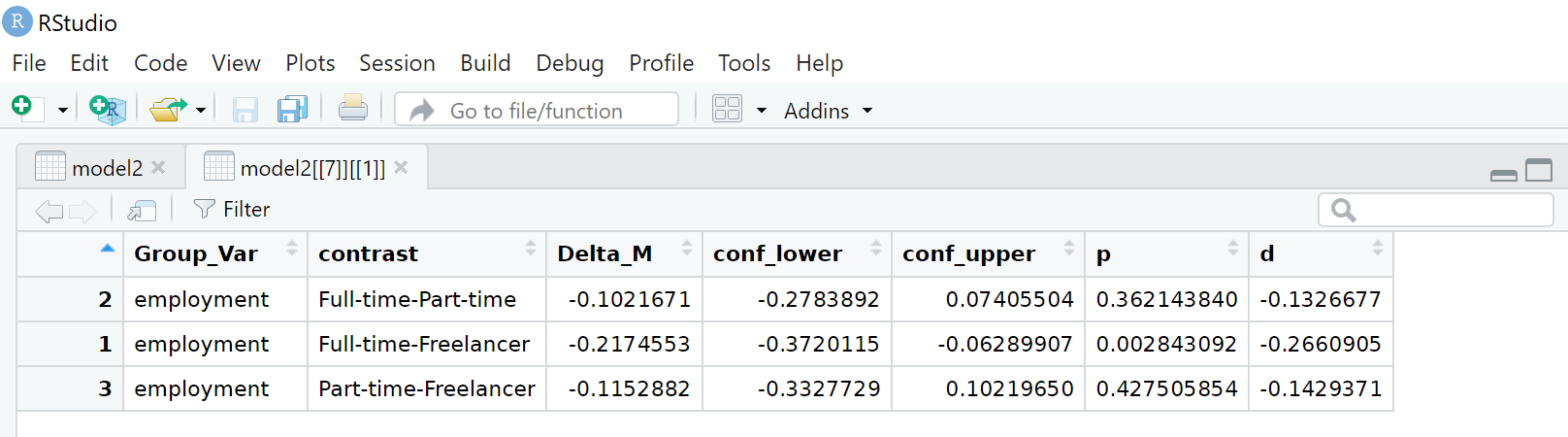
So wird deutlich, dass sich die Freelancer in ihrer Wahrnehmung mit hinreichender Sicherheit von den Vollzeitbeschäftigten (Full-time) unterscheiden, sonst gibt es keine signifikanten Unterschiede.

Alternativ kann der Post hoc-Test direkt ausgegeben werden:

Befehl:

WoJ %>%
  unianova(employment, autonomy_emphasis, post_hoc = TRUE) %>%
  dplyr::select(Variable, post_hoc) %>%
  tidyr::unnest(post_hoc)

Ausgabe:

# A tibble: 3 × 8
  Variable          Group_Var  contrast             Delta_M conf_lower conf_upper       p      d
  <chr>             <chr>      <chr>                  <dbl>      <dbl>      <dbl>   <dbl>  <dbl>
1 autonomy_emphasis employment Full-time-Part-time   -0.102     -0.278     0.0741 0.362   -0.133
2 autonomy_emphasis employment Full-time-Freelancer  -0.217     -0.372    -0.0629 0.00284 -0.266
3 autonomy_emphasis employment Part-time-Freelancer  -0.115     -0.333     0.102  0.428   -0.143

Visualisieren einer einfaktoriellen ANOVA

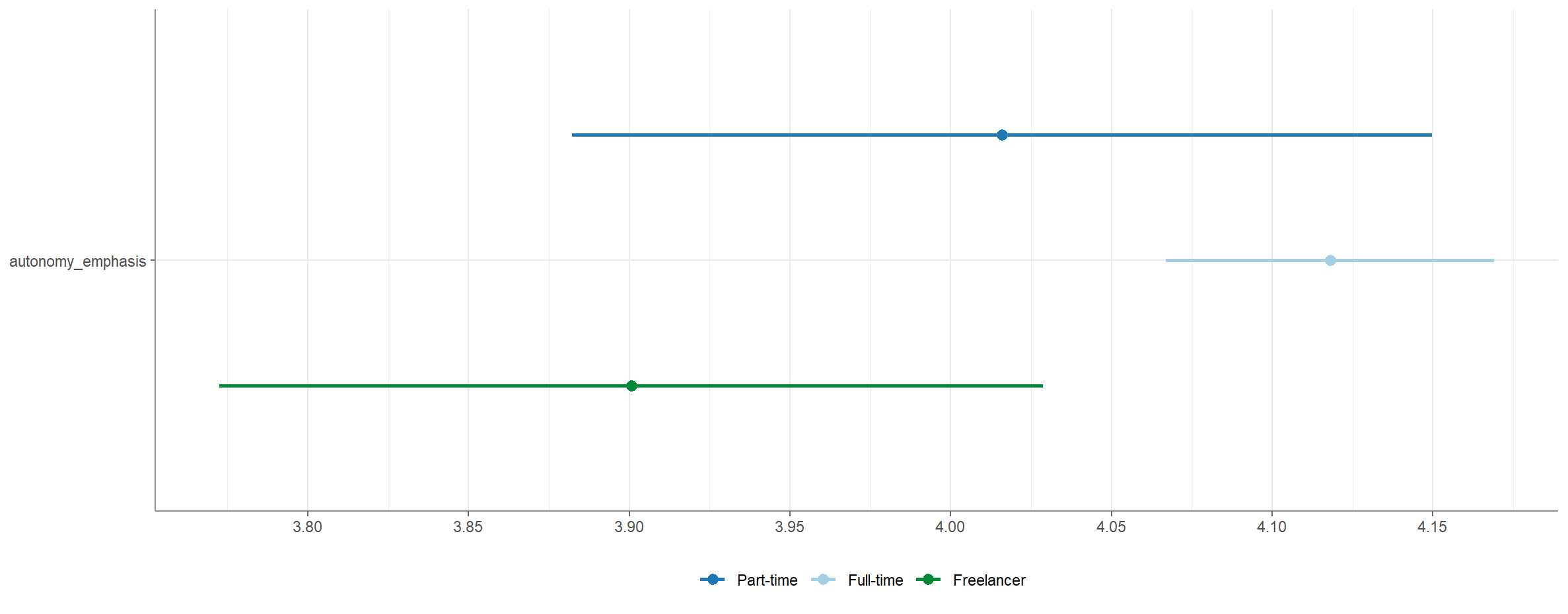
Eine Visualisierung ist über die Funktion visualize() möglich.

Befehl:

WoJ %>%
  unianova(employment, autonomy_emphasis) %>%
  visualize()

Ausgabe:

Einfaktoriellen ANOVA berichten

Notwendige Informationen

• Größe der Teilstichproben 1 (2): n₁ (n₂)
• Mittelwerte der Teilstichproben 1 (2): M₁ (M₂)
• Standardabweichungen der Teilstichproben 1 (2): SD₁ (SD₂)
• Kritischer F-Wert F_krit mit den Freiheitsgraden df_X und df_e
• Signifikanz und jeweiliges Signifikanzniveau des Zusammenhangs
• Varianzaufklärung η²
• Ergebnis des Post hoc-Tests
• Varianzhomogenität

Beispielbericht

„Mittels Varianzanalyse (Faktorstufen: Freelancer, Part-Time und Full-Time) konnte gezeigt werden, dass das Beschäftigungsverhältnis einen signifikanten Effekt auf die Wahrnehmung der Journalist:innen hat, wie autonom sie bei der Betonung sind, welche Aspekte einer Geschichte hervorgehoben werden. Der Faktor erklärt jedoch nur 1,0% der Varianz der abhängigen Variable.

Für den Post hoc_Test wurde Tukey’s HSD gerechnet, da Varianzhomogenität angenommen werden darf. Hier zeigt sich, dass die Freelancer signifikant weniger Autonomie wahrnehmen als ihre Kolleg:innen mit Full-time Job. Es gibt jedoch keinen signifikanten Unterschied zwischen den Freelancern und den Part-time Beschäftigten, die sich wiederum auch nicht von den Full-time Beschäftigten unterscheiden (n_Full-time = 898; M_Full-time = 4,12; SD_Full-time = 0,78; n_Part-time = 126; M_Part-time = 4,02; SD_Part-time = 0,76; n_Freelancer = 171; M_Freelancer = 3,90; SD_Freelancer = 0,85; F(2,1192) = 5,86; p = ,003; η² = ,010).”