Chi-Quadrat-Test

Was ist ein Chi-Quadrat-Test?

Der Chi-Quadrat-Test ist ein Signifikanztest, der verwendet wird, um zu prüfen, ob zwei kategoriale (d.h., nominale oder ordinale) Variablen voneinander unabhängig sind. Der Chi-Quadrat-Test basiert auf der Chi-Quadrat-Verteilung und prüft, ob sich die beobachteten Häufigkeiten signifikant von den erwarteten Häufigkeiten unterscheiden, also, ob es eine signifikante Abweichung vom Zufall gibt und damit einen Zusammenhang zwischen den beiden Variablen. „Kreuztabellen“ (oder auch: „Kontingenztabellen“) bilden die gemeinsamen Häufigkeitsverteilungen von zwei Variablen ab und sind damit grundlegend für das Verständnis des Chi-Quadrat-Tests.

Die Kreuztabelle…

• …kann sowohl absolute als auch relative Häufigkeiten abbilden.
• …ist geeignet für nominal- und ordinalskalierte Daten, aber auch für gruppierte metrische Variablen, sofern die Daten in dem Fall in Klassen zusammengefasst wurden.
• …besitzen 𝑘 Spalten und 𝑙 Zeilen, sodass sich 𝑘 × 𝑙 Zellen ergeben.
• …sind nach folgenden Konvention aufgebaut: Zur Untersuchung von gerichteten Zusammenhängen wird die unabhängige Variable (𝑋) als Spaltenvariable (d. h. „oben“) und die abhängige Variable (𝑌) als Zeilenvariable (d. h. „links“) dargestellt

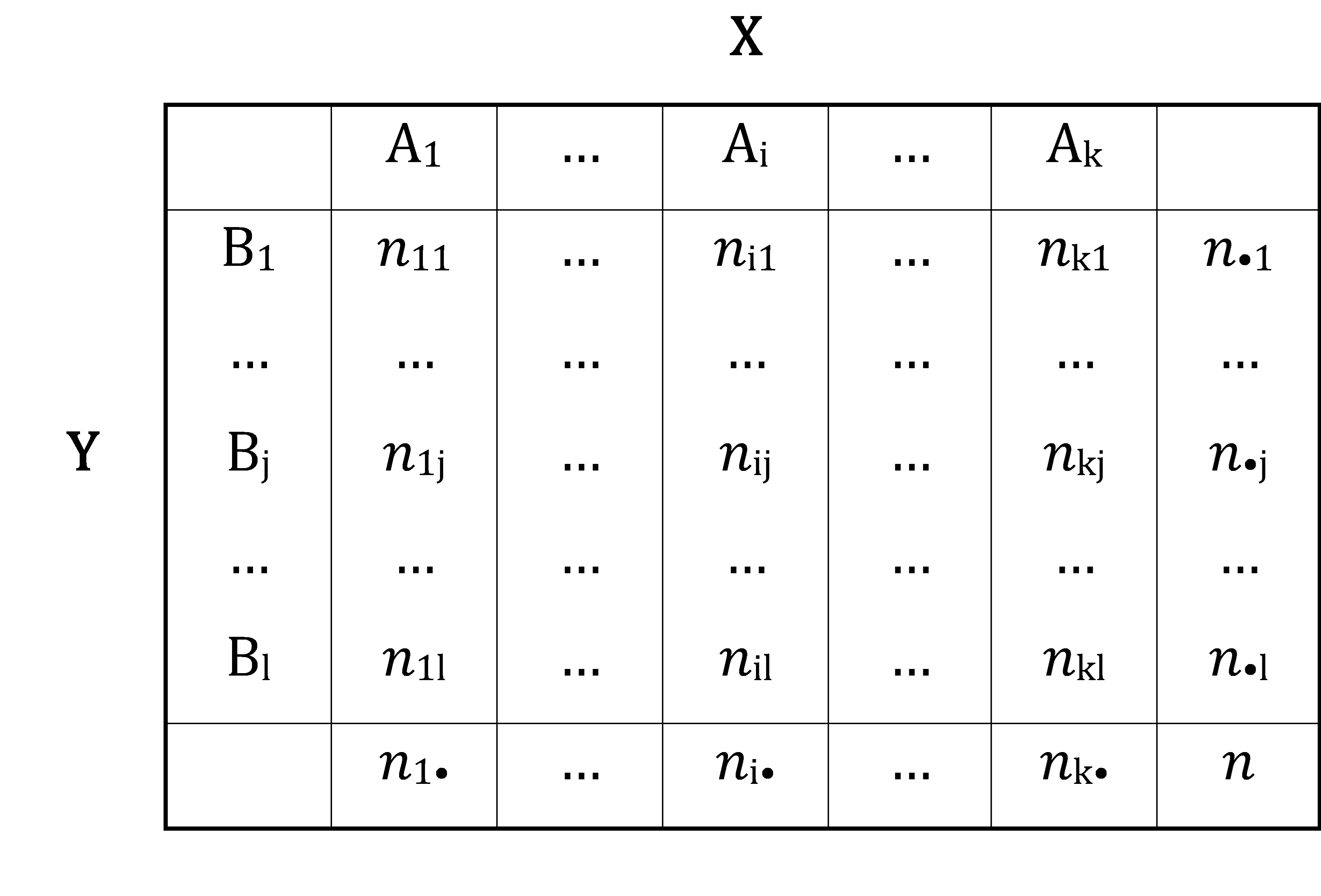
• 𝑛_𝑖𝑗 : Häufigkeit der Merkmalskombinationen
• 𝑛_𝑖• : Spaltensummen bzw. Randhäufigkeiten: (Unbedingte)Häufigkeit von Merkmal 𝐴_𝑖
• 𝑛_•𝑗 : Zeilensummen bzw. Randhäufigkeiten: (Unbedingte)Häufigkeit von Merkmal 𝐵_j

Die quadratische Kontingenz: Chi-Quadrat (χ²)…

• …bezeichnet die Größe des Zusammenhangs, allerdings nicht seine Stärke.
• …beruht auf dem Vergleich von beobachteten und erwarteten Häufigkeiten.
• …erfordert bei Unabhängigkeit von 𝑋 und 𝑌, dass das Unabhängigkeitskriterium für jedes 𝑛_𝑖𝑗 erfüllt ist.
• …hat einen Wertebereich von 0 bis unendlich. Bei χ²=0 sind Ereignisse völlig unabhängig, es gibt keinen Zusammenhang zwischen den Variablen.
• …ist bei ausreichend großen Stichproben annähernd χ²-verteilt mit 𝑑𝑓 = (𝑘 − 1) ∙ (𝑙 − 1) Freiheitsgraden.

Voraussetzungen

• Die Beobachtungen sind voneinander unabhängig.
• Maximal 20% aller Zellen der Tabelle weisen eine erwartete Häufigkeit kleiner als 5 auf (sonst droht eine Verfälschung von χ²). Ausweg: Zahl der Zellen (d. h. Kategorien) verringern, Ausprägungen zusammenfügen.
• Keine der erwarteten Häufigkeiten ist Null.

Berechnung von Chi-Quadrat

\chi^{2}=\sum_{i=1}^k\sum_{j=1}^l\frac{n_{ij}-e_{ij}}{e_{ij}}=\frac{n_{11}-e_{11}}{e_{11}}+\frac{n_{12}-e_{12}}{e_{12}}+...+\frac{n_{kl}-e_{kl}}{e_{kl}}

• 𝑘: Spaltennummer
• 𝑙: Zeilennummer
• 𝑛_𝑖𝑗: beobachtete Häufigkeit in der 𝑖-ten Spalte und 𝑗-ten Zeile, das sind also die jeweiligen Werte in den Zellen
• 𝑒_𝑖𝑗:erwartete Häufigkeit in der 𝑖-ten Spalte und 𝑗-ten Zeile, die erwartete Häufigkeit berechnet sich aus:

e_{ij}=\frac{n_{i•}\cdot n_{•j}}{N}=\frac{Spaltensumme_{(i)}\cdot Zeilensumme_{(j)}}{N}

Chi-Quadrat-Unabhängigkeitstest

Der Chi-Quadrat-Unabhängigkeitstest testet die Nullhypothese, dass es keinen signifikanten Zusammenhang gibt.

H_{0}:P_{ij}=P_{i•}\cdot P_{•j}

H_{1}:P_{ij}\neq P_{i•}\cdot P_{•j}

H₀ wird zum Signifikanzniveau α abgelehnt, falls χ² größer dem (1-α)-Quantil der Chi-Quadrat-Verteilung mit 𝑑𝑓 = (𝑘 − 1) ⋅ (𝑙 − 1) Freiheitsgraden ist
Die kritischen Chi-Quadrat-Werte werden aus der Chi-Quadrat-Verteilungstabelle abgelesen.

Ist der errechnete Chi-Quadrat-Wert größer als der kritische Chi-Quadrat-Wert, muss die Nullhypothese abgelehnt werden und die Alternativhypothese darf angenommen werden.

Zusammenhangsmaße

Phi-Koeffizient

• Zusammenhangsmaß für zwei dichotome Variablen (Vier-Felder-Tafel)
• Wertebereich: 0 (kein Zusammenhang) bis 1 (maximaler Zusammenhang)

Berechnung:

\phi=\sqrt{\frac{\chi^{2}}{N}}

Cramers 𝑉

• Zusammenhangsmaß für zwei nominalskalierte Variablen
• Variablen können beliebig viele Ausprägungen (d.h. Zeilen und Spalten in der Kontingenztabelle) haben
• Wertebereich: 0 (kein Zusammenhang) bis 1 (maximaler Zusammenhang)

Berechnung:

V=\sqrt{\frac{\chi^{2}}{N\cdot\left(R-1\right)}} \qquad mit \qquad R = min(k, l)

Es gilt: R = min(k, l); R ist immer die kleinere Anzahl, ist k also 2 und l ist 5, dann ist R gleich 2.

Interpretationskonvention

• Koeffizient < 0,1: Kein Zusammenhang
• Koeffizient ≥ 0,1: Geringer Zusammenhang
• Koeffizient ≥ 0,3: Mittlerer Zusammenhang
• Koeffizient ≥ 0,5: Hoher Zusammenhang
• Koeffizient ≥ 0,7: Sehr hoher Zusammenhang

Chi-Quadrat-Test in R

Deskriptive Statistik

Für die deskriptive Darstellung von Häufigkeiten eignet sich die tab_frequencies-Funktion aus dem tidycomm-Package. Sie tabelliert Häufigkeiten für eine oder mehrere kategorische Variablen, einschließlich relativer und kumulativer Häufigkeiten. Für den WoJ-Datensatz lassen sich so Häufigkeitstabellen erstellen.

Befehl:

WoJ %>% tab_frequencies(employment)

Ausgabe:

# A tibble: 3 × 5
  employment     n percent cum_n cum_percent
* <chr>      <int>   <dbl> <int>       <dbl>
1 Freelancer   172   0.143   172       0.143
2 Full-time    902   0.752  1074       0.895
3 Part-time    126   0.105  1200       1

Für den Chi-Quadrat-Test in R ist es sinnvoll die Häufigkeiten von Merkmalskombinationen ausgeben zu lassen, dafür wird einfach die zweite Variable ergänzt. Die Werte werden nicht als Kreuztabelle ausgegeben, sondern nach der ersten Variable in der Funktion sortiert.

Befehl:

WoJ %>% tab_frequencies(employment, reach)

Ausgabe:

 # A tibble: 12 × 6
   employment reach             n percent cum_n cum_percent
 * <chr>      <fct>         <int>   <dbl> <int>       <dbl>
 1 Freelancer Local            23 0.0192     23      0.0192
 2 Freelancer Regional         36 0.03       59      0.0492
 3 Freelancer National        104 0.0867    163      0.136 
 4 Freelancer Transnational     9 0.0075    172      0.143 
 5 Full-time  Local           111 0.0925    283      0.236 
 6 Full-time  Regional        287 0.239     570      0.475 
 7 Full-time  National        438 0.365    1008      0.84  
 8 Full-time  Transnational    66 0.055    1074      0.895 
 9 Part-time  Local            15 0.0125   1089      0.908 
10 Part-time  Regional         32 0.0267   1121      0.934 
11 Part-time  National         75 0.0625   1196      0.997 
12 Part-time  Transnational     4 0.00333  1200      1

Signifikanztest

Für die Berechnung von Chi-Quadrat-Tests wird die crosstab()-Funktion aus dem tidycomm-Package genutzt. Die crosstab()-Funktion berechnet eine Kontingenztabelle für eine unabhängige (Spalten-)Variable und eine oder mehrere abhängige (Zeilen-)Variablen. Wird das chi_square-Argument auf TRUE gesetzt, wird der Chi-Quadrat-Test und Cramer’s V berechnet.

Befehl:

WoJ %>% crosstab(reach, employment, chi_square = TRUE)

Ausgabe:

# A tibble: 3 × 5
  employment Local Regional National Transnational
* <chr>      <dbl>    <dbl>    <dbl>         <dbl>
1 Freelancer    23       36      104             9
2 Full-time    111      287      438            66
3 Part-time     15       32       75             4
# Chi-square = 16.005, df = 6, p = 0.014, V = 0.082

Wird das add_total-Argument auf TRUE gesetzt, wird zusätzlich die Zeilensumme ausgegeben. Wird das percentages-Argument auf TRUE gesetzt, werden die Spaltenprozente statt den absoluten Häufigkeiten ausgegeben. Die Argumente lassen sich einfach über ein Komma verketten.

Befehl:

WoJ %>% crosstab(reach, employment, add_total = TRUE, percentages = TRUE, chi_square = TRUE)

Ausgabe:

# A tibble: 3 × 6
  employment Local Regional National Transnational Total
* <chr>      <dbl>    <dbl>    <dbl>         <dbl> <dbl>
1 Freelancer 0.154   0.101     0.169        0.114  0.143
2 Full-time  0.745   0.808     0.710        0.835  0.752
3 Part-time  0.101   0.0901    0.122        0.0506 0.105
# Chi-square = 16.005, df = 6, p = 0.014, V = 0.082

Kreuztabellen berichten

Notwendige Informationen

• Tabellenbeschriftung und -Nummerierung, Tabellen sollten auf den ersten Blick verständlich sein
• Erklärung der dargestellten Werte (absolute Häufigkeiten, Prozentwerte etc.)
• ggf. zusätzliche Anmerkungen (z.B. Rundungsfehler, Beschreibung der Skala)
• Der Text sollte auf jede berichtete Tabelle rekurrieren
• In die Analyse eingegangene Fallzahl
• Chi-Quadrat-Wert
• Freiheitsgrade
• p-Wert
• Zusammenhangsmaß

Beispielbericht

„Die Studie konnte belegen, dass es zwar einen signifikanten Zusammenhang zwischen der Reichweite des Mediums und dem Beschäftigungsverhältnis von Journalist:innen gibt (N=1200; χ²=16,01; df=6; 𝑝<,05), jedoch ist die Stärke so gering (V=0,082), dass wir keinen Zusammenhang annehmen können.“