Korrelation

Die Korrelation ist ein statistisches Maß für die Stärke und Richtung der Wechselbeziehung zwischen zwei metrischen Variablen. Mithilfe einer Korrelation kann beschrieben werden, ob und wie metrische Merkmale zusammenhängen.
Zur Kausalität (etwa: ob Variable X dazu führt, dass sich Variable Y erhöht) kann keine Aussage getroffen werden.

Zusammenhänge zwischen zwei metrischen Variablen lassen sich graphisch mit Streudiagrammen (engl: „scatter plot“) veranschaulichen. Jedes Wertepaar eines Falls wird in einem Koordinatensystem als Punkt mit den Koordinaten (𝑥; 𝑦) dargestellt. Die x- und y-Achsen stehen dabei für die Ausprägung des Falls in den jeweiligen Variablen.

Typische Formen von Zusammenhängen:

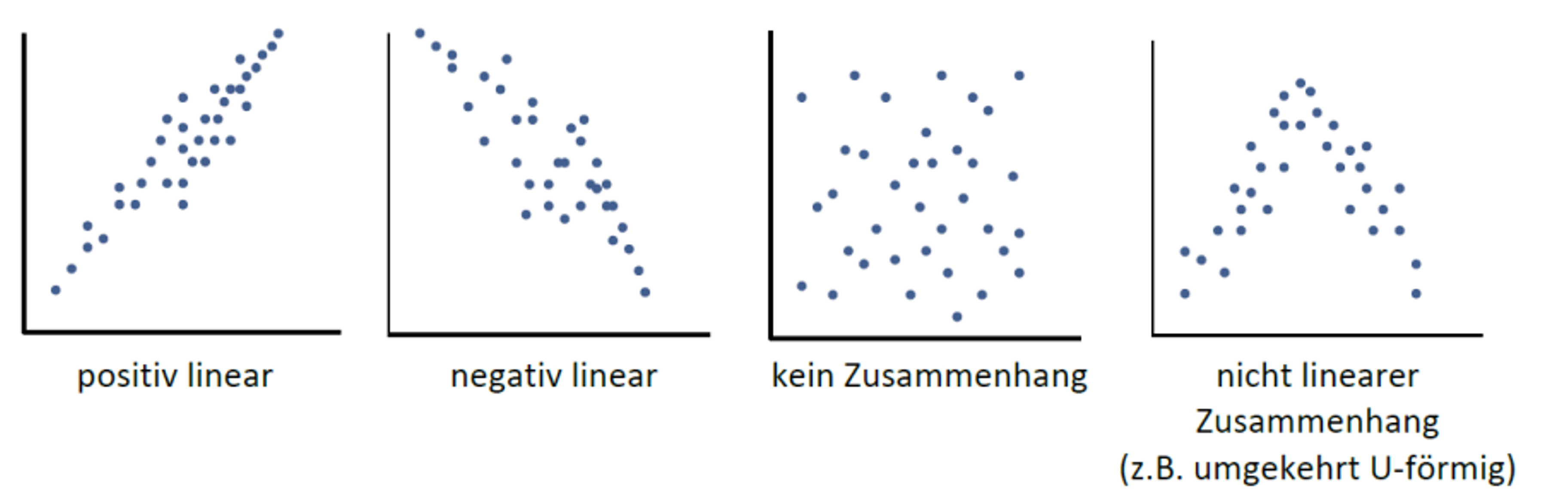
Der Berechnungsaufwand für die lineare Korrelation ist nur sinnvoll, wenn andere, nicht lineare Zusammenhänge (viertes Bild, ganz rechts) durch vorherige Begutachtung ausgeschlossen werden können. Deshalb sollte man sich vor einer Bestimmung der Korrelation immer das Streudiagramm ausgeben lassen.

Pearson-Korrelation

Ein häufig genutztes Maß für die Korrelation ist der Korrelationskoeffizient nach Auguste Bravais und Karl Pearson, auch „Produkt-Moment-Korrelation“, „Pearson-Korrelation“, oder „Pearson‘s 𝑟“ genannt. Der Korrelationskoeffizient wird dabei abgekürzt mit: 𝑟_𝑋𝑌.

Voraussetzungen

Für eine sinnvolle Interpretation müssen Voraussetzungen erfüllt sein:

• Die beiden Variablen müssen metrisch skaliert sein.
• Die beiden Variablen müssen normalverteilt sein.
• Der Zusammenhang zwischen beiden Variablen muss linear sein.

Berechnung der Pearson-Korrelation

Pearson‘s 𝑟 ergibt sich aus der standardisierten Kovarianz.

Die Kovarianz (𝑠_𝑋𝑌) ist eine über zwei Variablen definierte statistische Maßzahl für den linearen Zusammenhang zweier Variablen 𝑋 und 𝑌. Sie wird als wechselseitige Varianz zwischen diesen Variablen (Kreuzprodukt der Abweichungen vom Mittelwert) berechnet:

s_{XY}=\frac{1}{N-1}\sum_{i=1}^N (x_{i}-\bar{x})\cdot (y_{i}-\bar{y})

• s_XY : Kovarianz von X und Y
• N : Stichprobengröße
• x_i : Wert der Variable X von Fall i
• x̄ : arithmetisches Mittel der Variable X
• y_i : Wert der Variable Y von Fall i
• ȳ : arithmetisches Mittel der Variable Y

Der Betrag der Kovarianz ist klein, wenn sich die einzelnen Wertepaare nicht systematisch von ihren Mittelwerten unterscheiden. Je stärker sich die Werte der Kovarianz von Null unterscheiden, desto mehr liegt also eine lineare Beziehung vor.

• bei: s_XY > 0 eine positive lineare Beziehung
• bei: s_XY < 0: eine negative lineare Beziehung

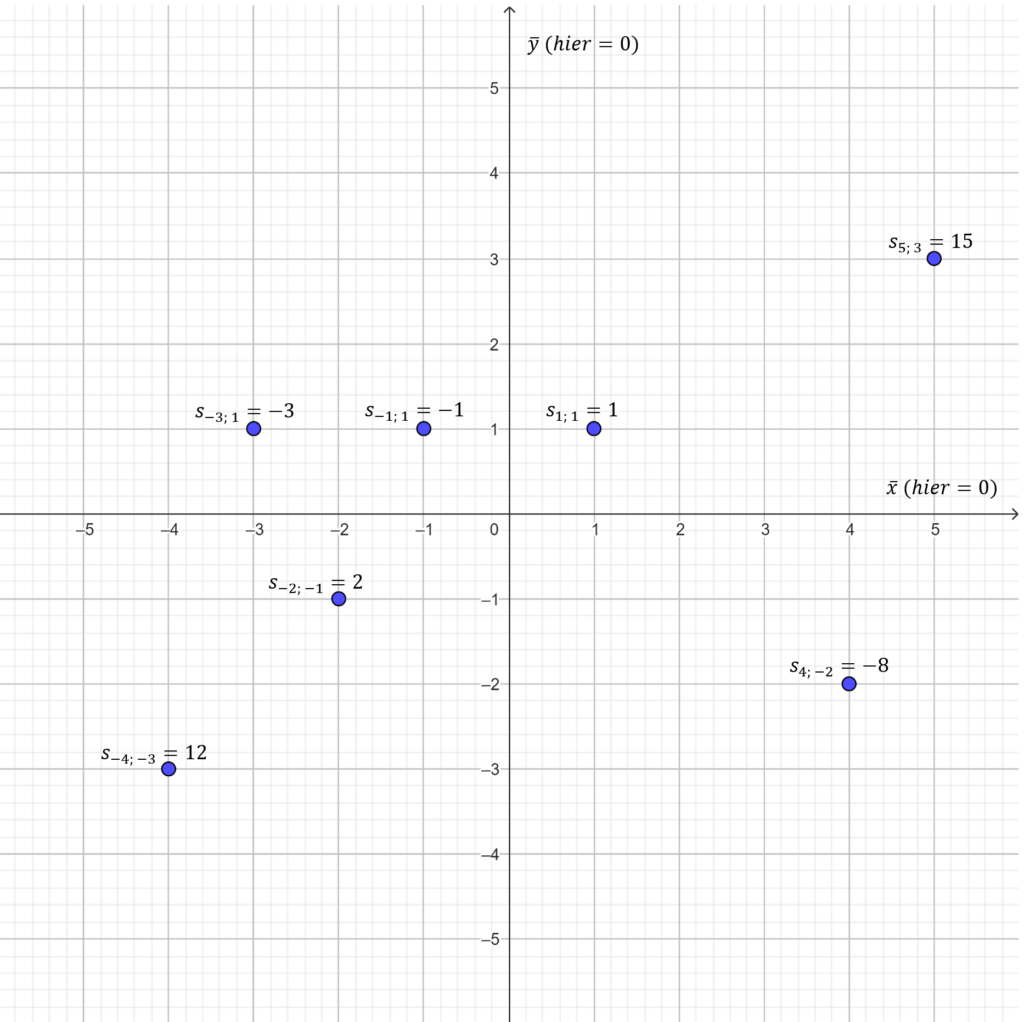
Zum einfachen Verständnis wie die Kovarianz funktioniert, kann man sich ein Streudiagramm vorstellen (siehe Bild), bei dem die Mittelwerte beider Variablen gleich Null sind; so lässt sich die Berechnung der Kovarianz schnell im Kopf durchführen. In dem Beispiel werden alle Werte addiert, was eine eine Kovarianz von 18 ergibt. Es liegt im Beispiel eine positive lineare Beziehung vor.

Kovarianzen lassen sich untereinander allerdings nicht vergleichen, da sie abhängig vom Maßstab bzw. dem Wertebereich der beobachteten Merkmale sind. Um Vergleichbarkeit herzustellen, benötigt es einen standardisierten Koeffizienten wie Pearson’s 𝑟. Diesen erhält man, indem die Kovarianz durch das Produkt der Standardabweichungen von X und Y geteilt wird.

s_{X}=\sqrt{s_X^2}=\sqrt{\frac{1}{N-1}\sum_{i=1}^N (x_{i}-\bar{x})^{2}}

s_{Y}=\sqrt{s_Y^2}=\sqrt{\frac{1}{N-1}\sum_{i=1}^N (y_{i}-\bar{y})^{2}}

• s_X : Standardabweichung von X
• s_Y : Standardabweichung von Y

Somit ist Pearson‘s 𝑟 (r_XY):

r_{XY}=\frac{s_{XY}}{s_{X}\cdot s_{Y}}

Wertebereich von r_XY

Der Wertebereich von Pearson‘s 𝑟 liegt zwischen -1 und +1.

• Ein Wert von +1 bedeutet, dass die beiden Variablen in einem perfekt positiven linearen Zusammenhang zueinander stehen. Ein positiver Zusammenhang liegt immer dann vor, wenn der Korrelationskoeffizient größer Null ist (r_XY > 0), es gilt: Je größer 𝑋, desto größer 𝑌 bzw. je kleiner 𝑋, desto kleiner 𝑌.
• Ein Wert von -1 bedeutet, dass die beiden Variablen in einem perfekt negativen linearen Zusammenhang zueinanderstehen (=inverses Verhältnis). Ein negativer Zusammenhang liegt immer dann vor, wenn der Korrelationskoeffizient kleiner Null ist (r_XY < 0), es gilt: Je größer 𝑋, desto kleiner 𝑌 bzw. je kleiner 𝑋, desto größer 𝑌.
• Ein Wert von 0 bedeutet, dass keine lineare Beziehung zwischen den beiden Variablen besteht, also kein linearer Zusammenhang vorliegt.

Interpretationskonvention

• Betrag des Koeffizienten < 0,1: „kein Zusammenhang“
• Betrag des Koeffizienten ≥ 0,1: „mindestens ein schwacher Zusammenhang“
• Betrag des Koeffizienten ≥ 0,3: „mindestens ein mittlerer Zusammenhang“
• Betrag des Koeffizienten ≥ 0,5: „mindestens ein starker Zusammenhang“
• Betrag des Koeffizienten ≥ 0,7: „sehr starker Zusammenhang“

Signifikanztest des Korrelationskoeffizienten r_XY

Um zu prüfen, ob ein Zusammenhang mit hinreichender Sicherheit auch in der Grundgesamtheit vorliegt, wird der Signifikanztest des Korrelationskoeffizienten r_XY gerechnet.

Die Nullhypothese nimmt keinen Zusammenhang an. Bei der Hypothesenformulierung wird nicht der Stichprobenkennwert r_XY geschrieben, sondern der Parameter 𝜌_XY (sprich: Rho von XY).

Zweiseitiges Problem:

H_{0}:\rho_{XY}=0

H_{1}:\rho_{XY}\neq0

Signifikanztest:

t=\frac{r_{XY}\cdot \sqrt{N-2}}{\sqrt{1-r_{XY}^2}} \qquad mit \qquad df=N-2

Testentscheidung nach festgelegtem Signifikanzniveau:

• Der kritische Wert 𝑡_{𝑘𝑟𝑖𝑡} kann unter Berücksichtigung des Signifikanzniveaus 𝛼 und der Freiheitsgrade 𝑑𝑓 aus der t-Verteilungstabelle, ausgelesen werden.
• 𝐻₀ wird abgelehnt, wenn |𝑡| > 𝑡_{𝑘𝑟𝑖𝑡}

Korrelation und Kausalität

Der Korrelationskoeffizient r_XY beschreibt den Zusammenhang nur für beobachtete Daten, also nur für die Stichprobe. Er gibt keinen Aufschluss über die Kausalrichtung (Wirkungsrichtung) eines Zusammenhangs.

Mögliche kausale Interpretation für eine Korrelation zwischen 𝑋 und 𝑌:

• 𝑋 beeinflusst 𝑌.
• 𝑌 beeinflusst 𝑋.
• 𝑋 und 𝑌 beeinflussen sich gegenseitig.

Ein Zusammenhang könnte aber auch durch eine oder mehrere andere Variable begründet sein. Es wird dann von einer Scheinkorrelation gesprochen. Dieses sogenannte Drittvariablenproblem – eine Drittvariable 𝑍 beeinflusst 𝑋 und 𝑌 – lässt sich durch die Berechnung partieller Korrelationskoeffizienten eingrenzen.

Partieller Korrelationskoeffizient

r_{XY|Z}=\frac{r_{XY}-r_{XZ}\cdot r_{YZ}}{\sqrt{1-r_{XZ}^2}\cdot \sqrt{1-r_{YZ}^2}}

Der partielle Korrelationskoeffizient beschreibt den Zusammenhang zwischen den Variablen 𝑋 und 𝑌, nachdem für den Einfluss der Drittvariablen 𝑍 kontrolliert wird. Das heißt, der Einfluss der Drittvariable wird „heraus gerechnet“. Mit dem partiellen Korrelationskoeffizienten lässt sich wie oben der Signifikanztest durchführen.

Weitere Arten von Korrelationen

Rangkorrelation: Zusammenhang zwischen ordinalskalierten (z. B.: „Zustimmung zu …“) und metrischen (z. B. „Lebensalter“) Merkmalen (z.B. Spearmans Rho, 𝜌 bzw. 𝑟_𝑠 oder Kendalls Tau, 𝜏)

Punktbiseriale Korrelation: Zusammenhang zwischen einer metrischen und einer dichotomen Variable (z. B. einer 0/1-codierten „Dummy“-Variable)

Korrelation in R

Die Funktion correlate() aus dem tidycomm-Package berechnet Korrelationskoeffizienten für alle Kombinationen der angegebenen Variablen. Die correlate()-Funktion gibt in einer Tabelle die Korrelationskoeffizienten, die jeweiligen Freiheitsgrade und die p-Werte an.

Möchte man nur für spezifische Variablen Korrelationen berechnen, so übergibt man die Variablennamen als Argumente. Für die drei ersten, quasi-metrisch skalierten Ethik-Variablen aus dem WoJ-Datensatz lassen sich so Korrelationen errechnen.

Befehl:

WoJ %>% correlate(ethics_1, trust_government, work_experience)

Ausgabe:

# A tibble: 3 x 6
  x                y                      r    df        p     n
* <chr>            <chr>              <dbl> <int>    <dbl> <int>
1 ethics_1         trust_government -0.102   1198 0.000421  1200
2 ethics_1         work_experience  -0.103   1185 0.000387  1187
3 trust_government work_experience  -0.0708  1185 0.0146    1187

Wenn keine Variablen angegeben werden, werden für alle numerischen (d. h. integer oder double) Variablen der jeweilige Korrelationskoeffizient, Freiheitsgrad und p-Wert ermittelt.

Befehl:

WoJ %>% correlate()

Ausgabe:

# A tibble: 55 × 5
   x                  y                        r    df         p
 * <chr>              <chr>                <dbl> <int>     <dbl>
 1 autonomy_selection autonomy_emphasis  0.644    1192 4.83e-141
 2 autonomy_selection ethics_1          -0.0766   1195 7.98e-  3
 3 autonomy_selection ethics_2          -0.0274   1195 3.43e-  1
 4 autonomy_selection ethics_3          -0.0257   1195 3.73e-  1
 5 autonomy_selection ethics_4          -0.0781   1195 6.89e-  3
 6 autonomy_selection work_experience    0.161    1182 2.71e-  8
 7 autonomy_selection trust_parliament  -0.00840  1195 7.72e-  1
 8 autonomy_selection trust_government   0.0414   1195 1.53e-  1
 9 autonomy_selection trust_parties      0.0269   1195 3.52e-  1
10 autonomy_selection trust_politicians  0.0109   1195 7.07e-  1
# ℹ 45 more rows
# ℹ Use `print(n = ...)` to see more rows

Mit der to_correlation_matrix()-Funktion werden die Korrelationen als Korrelationsmatrix ausgegeben.

Befehl:

WoJ %>%
  correlate() %>%
  to_correlation_matrix()

Ausgabe:

# A tibble: 11 × 12
   r                  autonomy_selection autonomy_emphasis ethics_1 ethics_2 ethics_3 ethics_4 work_experience trust_parliament trust_government trust_parties trust_politicians
 * <chr>                           <dbl>             <dbl>    <dbl>    <dbl>    <dbl>    <dbl>           <dbl>            <dbl>            <dbl>         <dbl>             <dbl>
 1 autonomy_selection            1                 0.644   -0.0766  -0.0274   -0.0257 -0.0781          0.161           -0.00840           0.0414        0.0269           0.0109 
 2 autonomy_emphasis             0.644             1       -0.114   -0.0337   -0.0297 -0.127           0.155           -0.00465           0.0268        0.0102           0.00242
 3 ethics_1                     -0.0766           -0.114    1        0.172     0.165   0.343          -0.103           -0.0378           -0.102        -0.0472          -0.00725
 4 ethics_2                     -0.0274           -0.0337   0.172    1         0.409   0.321          -0.168            0.00161           0.0374        0.0238           0.0250 
 5 ethics_3                     -0.0257           -0.0297   0.165    0.409     1       0.273          -0.0442          -0.0486           -0.0743       -0.0115          -0.0212 
 6 ethics_4                     -0.0781           -0.127    0.343    0.321     0.273   1              -0.116           -0.0632           -0.0733       -0.0309          -0.00218
 7 work_experience               0.161             0.155   -0.103   -0.168    -0.0442 -0.116           1               -0.00941          -0.0708       -0.0454          -0.00976
 8 trust_parliament             -0.00840          -0.00465 -0.0378   0.00161  -0.0486 -0.0632         -0.00941          1                 0.680         0.536            0.549  
 9 trust_government              0.0414            0.0268  -0.102    0.0374   -0.0743 -0.0733         -0.0708           0.680             1             0.591            0.548  
10 trust_parties                 0.0269            0.0102  -0.0472   0.0238   -0.0115 -0.0309         -0.0454           0.536             0.591         1                0.711  
11 trust_politicians             0.0109            0.00242 -0.00725  0.0250   -0.0212 -0.00218        -0.00976          0.549             0.548         0.711            1      

Zuletzt können durch Angabe des with-Parameters gezielt Variablen mit einer Fokusvariable korreliert werden.

Befehl

WoJ %>% correlate(with = work_experience)

Ausgabe

# A tibble: 10 x 6
   x               y                         r    df             p     n
 * <chr>           <chr>                 <dbl> <int>         <dbl> <int>
 1 work_experience autonomy_selection  0.161    1182 0.0000000271   1184
 2 work_experience autonomy_emphasis   0.155    1180 0.0000000887   1182
 3 work_experience ethics_1           -0.103    1185 0.000387       1187
 4 work_experience ethics_2           -0.168    1185 0.00000000619  1187
 5 work_experience ethics_3           -0.0442   1185 0.128          1187
 6 work_experience ethics_4           -0.116    1185 0.0000602      1187
 7 work_experience trust_parliament   -0.00941  1185 0.746          1187
 8 work_experience trust_government   -0.0708   1185 0.0146         1187
 9 work_experience trust_parties      -0.0454   1185 0.118          1187
10 work_experience trust_politicians  -0.00976  1185 0.737          1187

Partieller Korrelationskoeffizient in R

Um den partiellen Korrelationskoeffizienten zu berechnen, wird die unabhängige Variable X und die abhängige Variable Y sowie die Variable Z im optionalen Parameter partial hinzugefügt. Die Funktion kontrolliert dann die im partial-Parameter angegebene Z-Variable.

Befehl:

WoJ %>% correlate(ethics_1, trust_government, partial = work_experience)

Ausgabe:

# A tibble: 1 x 7
  x        y                z                    r    df        p     n
* <chr>    <chr>            <chr>            <dbl> <dbl>    <dbl> <int>
1 ethics_1 trust_government work_experience -0.111  1184 0.000124  1187

Weitere Arten von Korrelationen in R

Um eine andere Korrelationsart zu berechnen, wird der optionale Parameter method = "kendall" oder method = "spearman" hinzugefügt. Der Parameter Method ist standartmäßig gleich "pearson".

Befehl:

WoJ %>% correlate(ethics_1, ethics_2 , method = "kendall")

Ausgabe:

# A tibble: 1 × 5
  x        y          tau df           p
* <chr>    <chr>    <dbl> <lgl>    <dbl>
1 ethics_1 ethics_2 0.159 NA    1.56e-10

Visualisierung von Korrelationen in R

Mit der visualize()-Funktion lassen sich die Korrelationen graphisch darstellen.

Visualisieren der Korrelation von zwei Variablen

Befehl:

WoJ %>%
  correlate(ethics_1, autonomy_selection) %>%
  visualize()

Ausgabe:

Visualisieren der Korrelation von mehreren Variablen

Befehl:

WoJ %>%
  correlate(ethics_1, autonomy_selection, work_experience) %>%
  visualize()

Ausgabe:

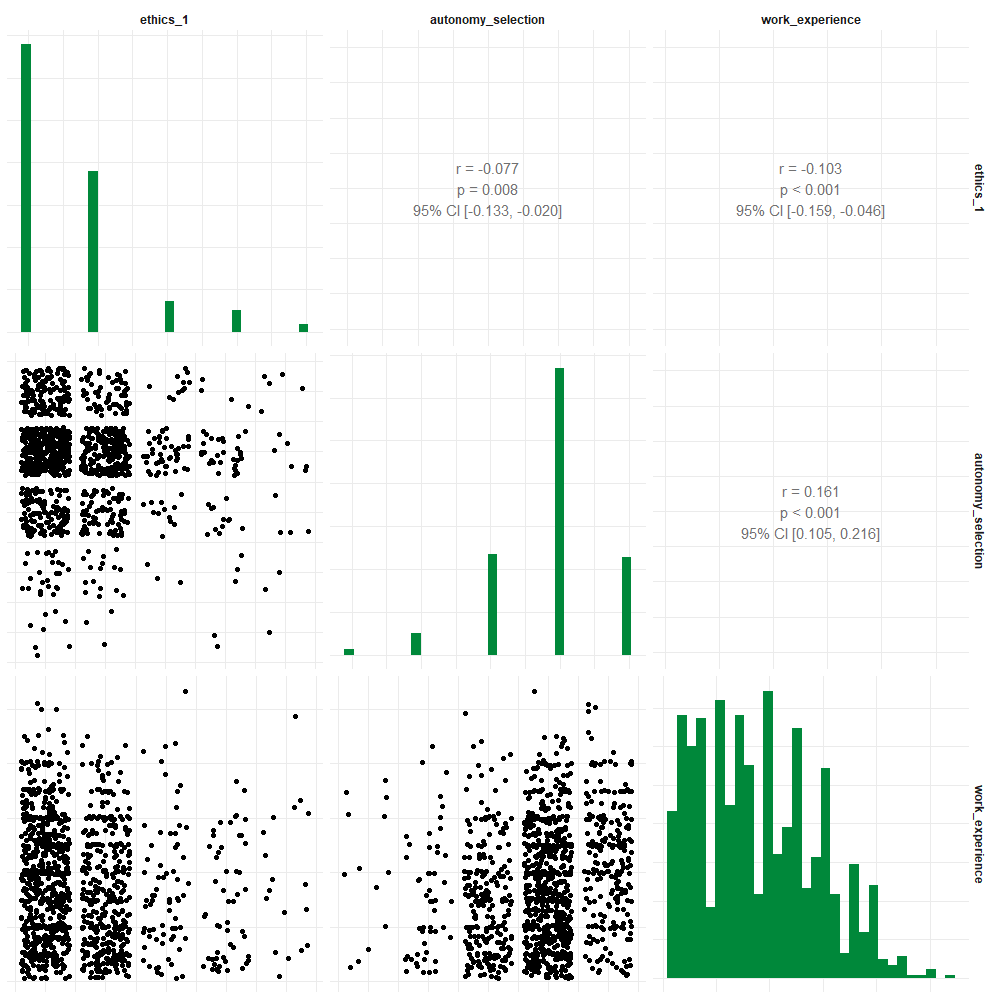
Visualisieren einer partiellen Korrelation

Befehl:

WoJ %>%
  correlate(ethics_1, autonomy_selection, work_experience, partial = TRUE) %>%
  visualize()

Ausgabe:

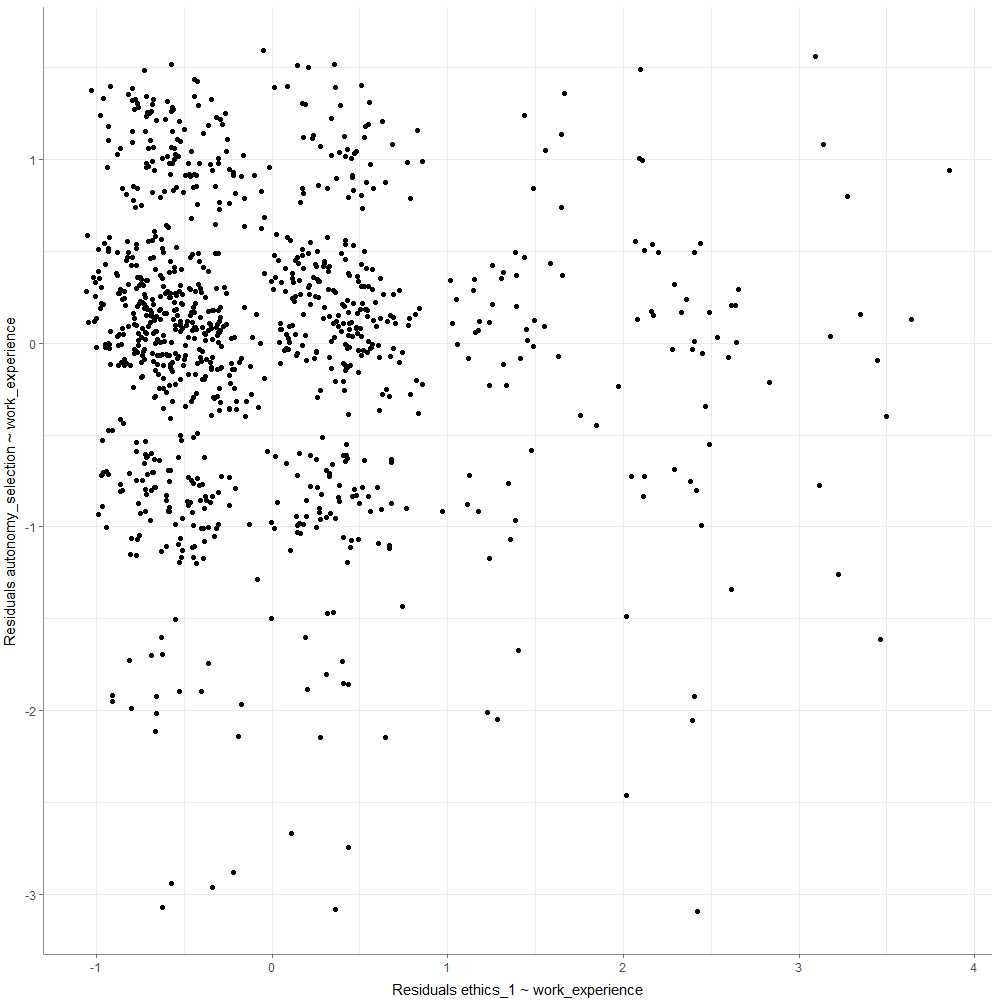
Korrelationen berichten

Notwendige Informationen

• Stärke des Zusammenhangs
• Richtung des Zusammenhangs
• Signifikanz und jeweiliges Signifikanzniveau des Zusammenhangs
• Informationen zur Stichprobengröße (N oder df)

Beispielbericht

„Es zeig sich eine signifikante, aber schwach ausgeprägte negative Beziehung zwischen der Berufserfahrung in Jahren und der ethischen Bewertung („Was im Journalismus ethisch ist, hängt von der jeweiligen Situation ab“) (N = 1187; r = -,103; p < ,001). …“