Logo IfKW

Normalverteilung

Die sogenannte Normalverteilung ist wohl die bekannteste stetige Wahrscheinlichkeitsverteilung. Sie wurde von Abraham de Moivre (1667-1754) und Pierre‐Simon Laplace (1749-1827) als Annäherung an die Binomialverteilung entwickelt. Am häufigsten wird sie mit Carl Friedrich Gauß (1777-1855) in Verbindung gebracht, der die Normalverteilung unter anderem in der Astronomie einsetzte.

Graph der Normalverteilung: Symmetrische, gerade und glockenförmige Verteilung.
Normalverteilung

Eigenschaften

  • Normalverteilungen sind symmetrisch und eingipflig.
  • Erwartungswert, Median und Modus sind identisch, liegen genau in der Mitte und teilen die Verteilung exakt in zwei Hälften.
  • Die meisten Werte streuen nah um den Erwartungswert.
  • Normalverteilungen nähern sich der 𝑋‐Achse an, ohne sie zu berühren.
  • Normalverteilungen sind durch zwei Größen eindeutig bestimmt, nämlich durch den Erwartungswert und die Standardabweichung. Die Schreibweise ist: 𝑁(𝜇; 𝜎)
  • Der Definitionsbereich (𝑋-Achse) reicht von − ∞ bis + ∞.
  • Die Standartnormalverteilung ist: N(0;1)
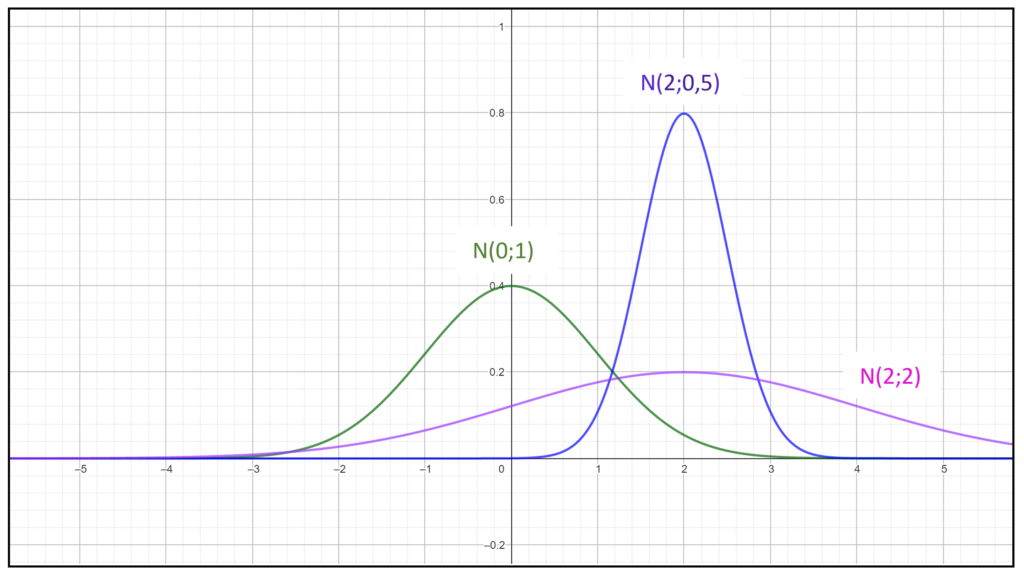
Drei Graphen der Normalverteilung in einem Koordinatensystem. Einmal in Grün die Standardnormalverteilung definiert durch den Mittelwert Null und die Standartabweichung eins. Und zwei weitere Beispiele für Normalverteilungen: Eine spitzere Normalverteilung mit der Standartabweichung 0,5 und eine flachere Normalverteilung mit der Standartabweichung 2, beide haben den Mittelwert 2, das Maximum ist also nach rechts verschoben.
Normalverteilungen

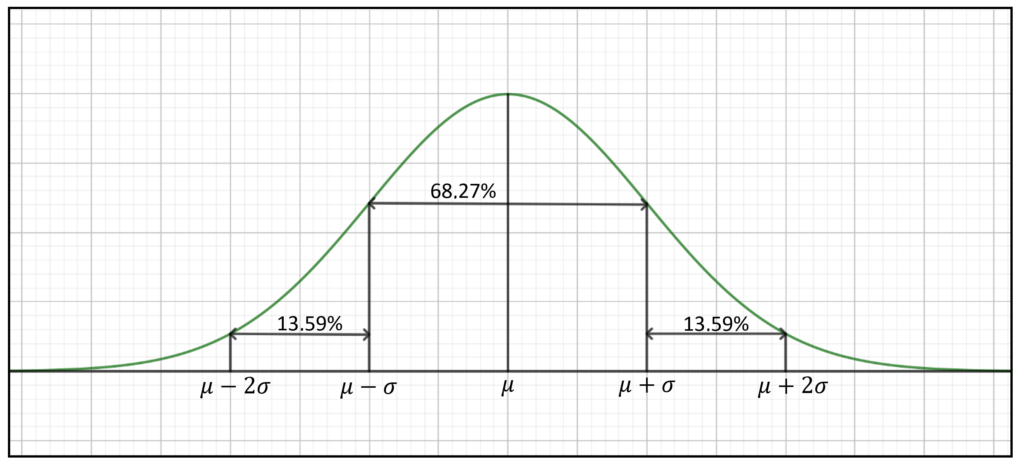
Dichtefunktion

Die Fläche, die von ± einer Standardabweichung vom Erwartungswert begrenzt wird, beinhaltet mehr als 2/3 aller Fälle (68,3%)
95,4% liegen im Bereich von ± 2 Standardabweichungen
99,7 % liegen im Bereich von ± 3 Standardabweichungen

Dichtefunktion: Graph der Standardnormalverteilung unterteilt in fünf Bereiche. Die x-Achse ist mit den Parametern My für den Mittelwert und Sigma für die Standardabweichung beschriftet. 68,27 Prozent der Fläche unter dem Graphen sind im Bereich von einer Standardabweichung um den Mittelwert. Jeweils 13,59 Prozent sind dann nochmal bis zu zwei Standardabweichungen vom Mittelwert entfernt. Die übrigen 4,55 Prozent sind weiter als zwei Standardabweichungen vom Mittelwert entfernt. Bei Normalverteilungen finden sich die meisten Werte finden also nahe am Mittelwert.
Dichtefunktion der Standardnormalverteilung

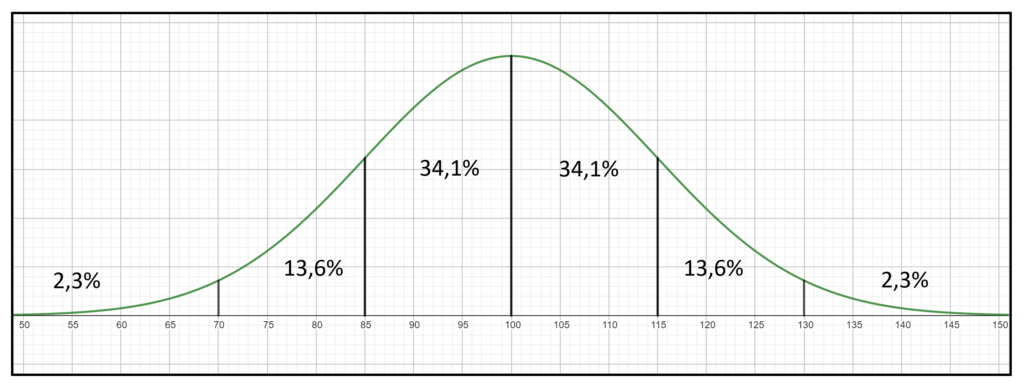
Beispiel: Intelligenzquotient (IQ)

Der IQ ist normalverteilt: 𝑁(100; 15)

68% haben einen IQ zwischen 85 und 115 (100 ± 15)

95% haben einen IQ zwischen 70 und 130 (100 ± 2·15)

Beispiel Intelligenzquotient: Graph der Normalverteilung unterteilt in sechs Bereiche. Bis 70 Punkte haben nur 2,3 Prozent, zwischen 70 und 85 Punkten haben 13,6 Prozent, zwischen 85 und 100 Punkten haben 34,1 Prozent, zwischen 100 und 115 Punkten haben 34,1 Prozent, zwischen 115 und 130 Punkten haben 13,6 Prozent und mehr als 130 Punkte haben wiederum nur 2,3 Prozent. Die Abstände auf der Punkte-Achse sind also immer gleich und die Häufigkeiten sind symmetrisch zum Mittelwert von 100 Punkten.
Verteilung des Intelligenzquotienten

Standardnormalverteilung

Die Standardnormalverteilung ist ein Sonderfall der Normalverteilung: 𝑁(0; 1)
Jede Normalverteilung lässt sich mithilfe der 𝑧‐Transformation in die Standardnormalverteilung transformieren. Dabei werden die Verteilungswerte in 𝑧‐Werte standardisiert

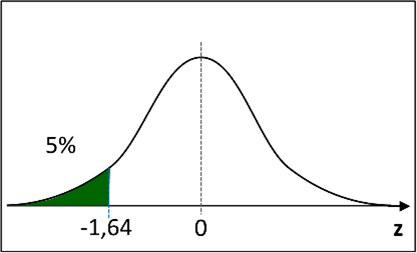
Graph einer Standardnormalverteilung in einem Koordinatensystem: Symmetrische, gerade und glockenförmige Verteilung, mit Maximum bei einem z von null und einer Standardabweichung von eins. Bei einem z von -1,64 sind links 5 Prozent der Fläche unter dem Graphen eingeschlossen und in grün farblich hervorgehoben.
Bei einem z von -1,64 sind links 5 Prozent der Fläche unter dem Graphen eingeschlossen.
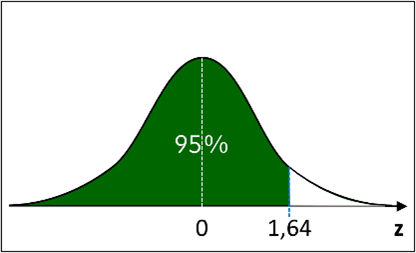
Graph einer Standardnormalverteilung in einem Koordinatensystem: Symmetrische, gerade und glockenförmige Verteilung, mit Maximum bei einem z von null und einer Standardabweichung von eins. Bei einem z von und 1,64 sind links 95 Prozent der Fläche unter dem Graphen eingeschlossen und in grün farblich hervorgehoben.
Bei einem z von und 1,64 sind links 95 Prozent der Fläche unter dem Graphen eingeschlossen.
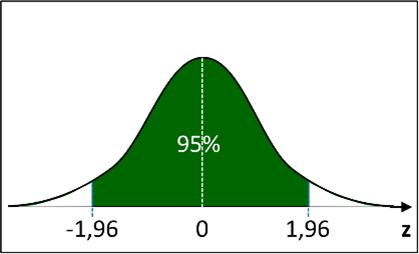
Graph einer Standardnormalverteilung in einem Koordinatensystem: Symmetrische, gerade und glockenförmige Verteilung, mit Maximum bei einem z von null und einer Standardabweichung von eins. Zwischen einem z von -1,96 und 1,96 sind in der Mitte 95 Prozent der Fläche unter dem Graphen eingeschlossen und in grün farblich hervorgehoben.
Zwischen einem z von -1,96 und 1,96 sind in der Mitte 95 Prozent der Fläche unter dem Graphen eingeschlossen.


Wie bei allen stetigen Verteilungen wird die Fläche unterhalb der Kurve auf 100% gesetzt. Somit entspricht jedem 𝑧-Wert (bzw. einer Differenz aus 𝑧-Werten) ein bestimmter Flächenanteil.

Bedeutung

  • Viele empirische Merkmale folgen einer Normalverteilung, beispielsweise der altersspezifische IQ, Körpergewicht und -größe oder die tägliche Rendite von Aktien der Deutschen Bank.
  • Bei genügend großen Stichproben folgt die Verteilung von Mittelwerten (bei multiplen Stichprobenziehungen) einer Normalverteilung (siehe Zentraler Grenzwertsatz). Daher wird die Normalverteilung verwendet, um von Stichproben auf die Verteilung eines Merkmals in der Grundgesamtheit zu schließen.
  • Viele andere Wahrscheinlichkeitsverteilungen können durch die Normalverteilung angenähert werden (z.B. Binomial- oder 𝑡-Verteilung).