Die Regression ist ein statistisches Verfahren zur Untersuchung des Zusammenhangs zwischen einer abhängigen Variable (AV) und einer oder mehreren unabhängigen Variablen (UV). Die abhängige Variable ist die Variable, die „erklärt werden“ soll, und die unabhängigen Variablen sind die Variablen, die dies „leisten „Erklärung“ leisten sollen.
Man spricht in diesem Kontext auch von einem Zurückführen eines Kriteriums (vorherzusagende abhängige Variable Y) auf einen oder mehrere Prädiktoren (beeinflussende unabhängige Variablen X1, X2, etc.).
Damit postuliert die Regression einen Zusammenhang, der in eine bestimmte Richtung verläuft. Es muss hier also, anders als bei der Korrelation, eine Vermutung zur Kausalität vorliegen, um sinnvoll vorgehen zu können.
Mit der linearen Regression werden lineare Zusammenhänge erklärt. Es gibt auch weitere Methoden und Arten, angenommene (auch nicht-lineare) Zusammenhänge zu erklären, wie zum Beispiel die logistische Regression.
Lineare Regression
Bei der linearen Regression sind die Variablen metrisch skaliert. Das vorher zu inspizierende Streudiagramm legt einen linearen Zusammenhang nahe.
Es werden bei der linearen Regression zwei Typen unterschieden:
a) Einfache bzw. bivariate Regression mit nur einem Prädiktor
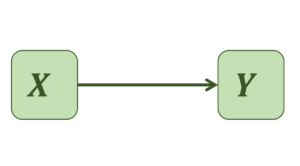
b) Multiple Regression mit zwei und mehr Prädiktoren
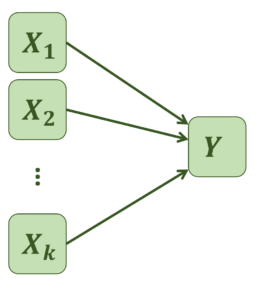
a) Einfache lineare Regression
Ziel der einfachen linearen Regression ist das Auffinden einer linearen Funktion, die die Verteilung der Wertepaare (xi ; yi) im Streudiagramm möglichst gut abbildet, Das heißt: das Finden der Regressionsgerade, von der diese Wertepaare möglichst wenig abweichen.
Lineare Regressionsfunktion:
y_{i}=a+b\cdot x_{i}+e_{i}𝑦𝑖 = beobachteter 𝑌‐Wert für den 𝑋‐Wert der 𝑖‐ten Beobachtung
𝑎 = Schnittpunkt mit der 𝑌‐Achse (Achsenabschnitt bzw. „Konstante“)
𝑏 = Steigung der Regressionsgeraden (unstandardisierter Regressionskoeffizient)
𝑒𝑖 = Residuum bzw. Abweichung des beobachteten Werts 𝑦𝑖 vom vorhergesagten Wert ŷi (𝑒=„error“)
Beispiel
Forscher:innen vermuten, dass Paare, welche angeben, sich mehr zu lieben, auch länger miteinander kommunizieren. Auf der x-Achse ist die „Liebe“-Skala (0: sehr niedriger Liebeswert, 20: sehr hoher Liebeswert) und auf der y-Achse die tägliche Kommunikation in Minuten abgetragen. Mit einer kleinen Umfrage unter 10 Paaren erhalten die Forscher:innen folgende Werte.
| Probanden-Paar (i) | Punkte auf der „Liebe“-Skala (xi) | Tägliche Kommunikation in Minuten (yi) |
| 1 | 9 | 4 |
| 2 | 15 | 30 |
| 3 | 13 | 9 |
| 4 | 10 | 8 |
| 5 | 0 | 1 |
| 6 | 9 | 6 |
| 7 | 5 | 5 |
| 8 | 12 | 10 |
| 9 | 1 | 0 |
| 10 | 11 | 7 |
| Mittelwert | 8,5 | 8,0 |
| s | 4,99 | 8,38 |
Diese Werte lassen sich auch als Punktewolke bzw. Streudiagramm darstellen:
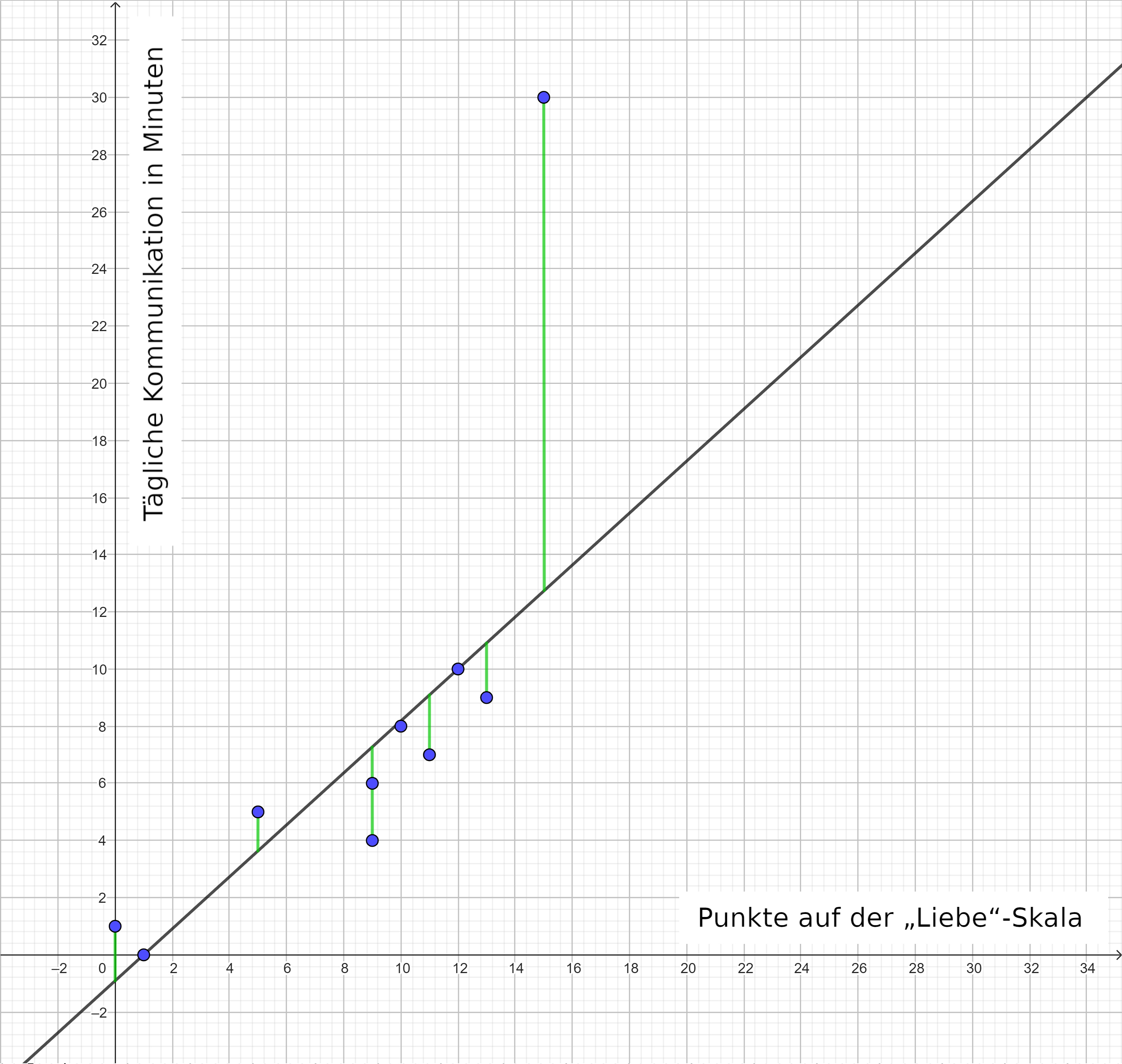
Die Gerade der linearen Regressionsfunktion wird so gewählt, dass die Abweichung der erwarteten Werte von den beobachteten Werten minimal ist. Diese Abweichungen sind hier in grün dargestellt. Eine Methode, um die Regressionsgerade zu berechnen, ist die Methode der kleinsten Quadrate (OLS = Ordinary Least Squares), welche die Summe der quadrierten Residuen minimiert:
\sum_{i=1}^N e_i^2 \qquad mit \qquad e_i=y_{i}-\hat{y_{i}} =y_{i}-(a+b\cdot x_{i})Berechnung der Parameter einer einfachen linearen Regressionsfunktion
Da für die saubere Herleitung der Methode der kleinsten Quadrate (OLS= Ordinary Least Squares) partielle Ableitungen nötig sind, sind Interessierte an gute Quellen im Internet verwiesen. Ein separater Exkurs mit einer Einführung der Differenzialrechnung erfolgt an dieser Stelle nicht, vorgestellt wird nur das Ergebnis.
Die Steigung berechnet sich somit aus der Kovarianz von X und Y durch die Varianz von X.
b=\frac{s_{XY}}{s_X^2}Nachdem die lineare Regressionsfunktion durch den Punkt (ȳ; x̄) verläuft, ergibt sich für den y-Achsenabschnitt a:
a=\bar{y}-b\cdot \bar{x}Die Parameter der linearen Regressionsfunktion im Streudiagramm:
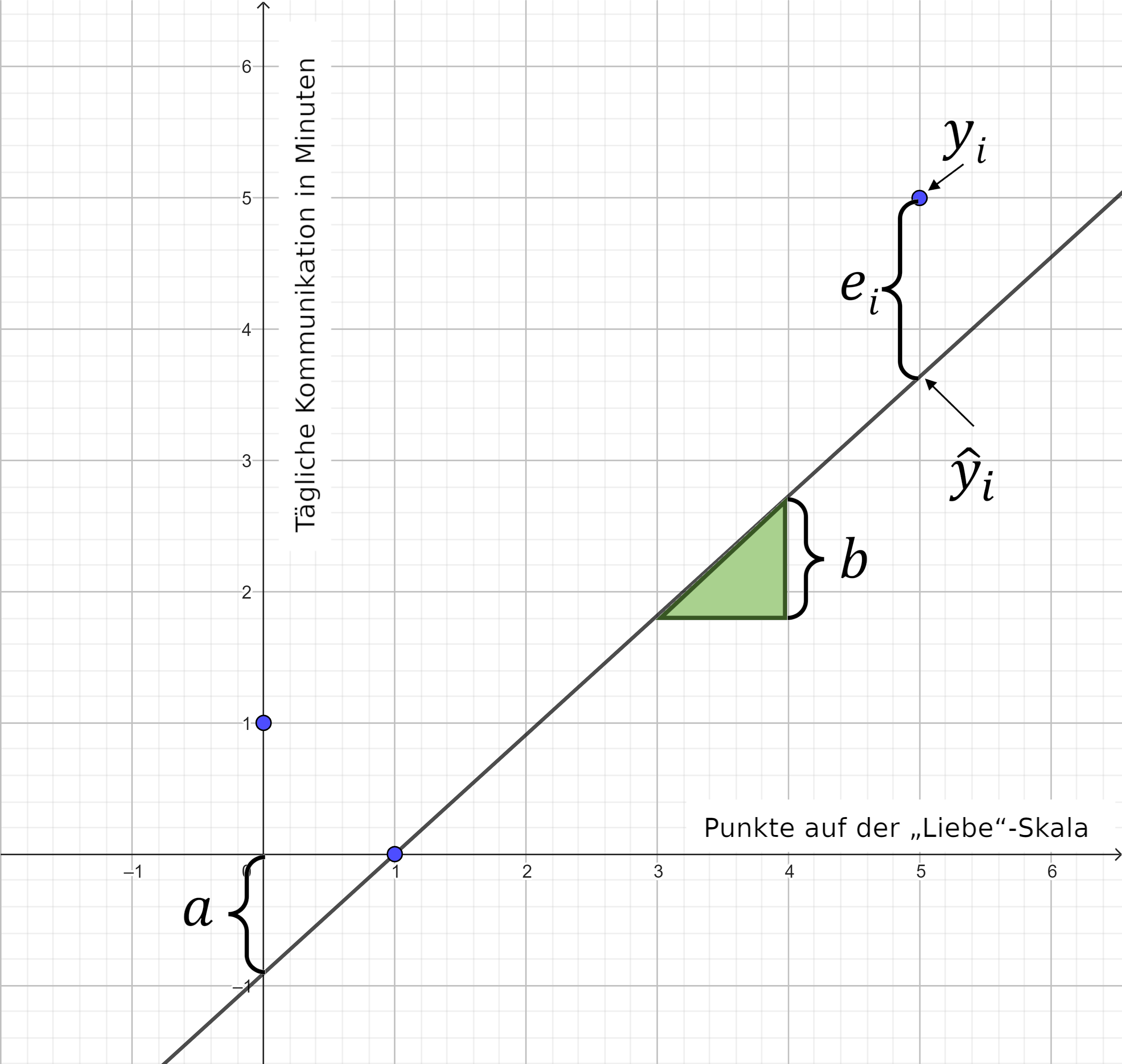
Für das Beispiel ergibt sich:
s_{XY}(Kovarianz)=\frac{1}{N-1}\cdot\sum_{i=1}^N(x_{i}-\bar{x})\cdot(y_{i}-\bar{y})=\frac{279}{9}=31s_X^2(Varianz\,von\,X)=\frac{1}{N-1}\cdot\sum_{i=1}^N(x_{i}-\bar{x})^{2}=\frac{224,5}{9}=24,94b=\frac{s_{XY}}{s_X^2}=\frac{31}{24,94}=1,24a=\bar{y}-b\cdot \bar{x}=8,0-1,24\cdot 8,5=-2,56…und damit ist die lineare Regressionsfunktion:
\hat{y_{i}}=-2,56+1,24\cdot x_{i}In diesem Kontext bedeutet dies auf das Beispiel bezogen: „Ein um einen Punkt größerer Wert auf der „Liebe-Skala“ entspricht täglich 1,24 Minuten längerer Kommunikation in der Partnerschaft“.
Standardisierung von Regressionskoeffizienten
Der unstandardisierte Regressionskoeffizient b ist abhängig vom Wertebereich von X und Y. Wenn Regressionskoeffizienten miteinander verglichen werden sollen, beispielsweise bei der multiplen Regression, ist eine Standardisierung der Koeffizienten notwendig.
Berechnung:
\beta=b\cdot\frac{s_{X}}{s_Y}β hat einen Wertebereich von 0 bis 1.
Für das Beispiel ist:
\beta=b\cdot\frac{s_{X}}{s_Y}=1,24\cdot\frac{4,99}{8,38}=0,74Zum Vergleich: Der Korrelationskoeffizient rXY = 0,74 ist nicht immer mit β identisch. Dass β gleich rXY ist, gilt nur für die einfache lineare Regression. Da rXY teils einfacher als β zu berechnen ist, kann dies Zeit sparen.
Interpretationskonvention
- Betrag des Koeffizienten < 0,1: „kein Einfluss des Prädiktors auf das Kriterium“
- Betrag des Koeffizienten ≥ 0,1: „mindestens ein schwacher Einfluss des Prädiktors auf das Kriterium“
- Betrag des Koeffizienten ≥ 0,3: „mindestens ein mittlerer Einfluss des Prädiktors auf das Kriterium“
- Betrag des Koeffizienten ≥ 0,5: „mindestens ein starker Einfluss des Prädiktors auf das Kriterium“
- Betrag des Koeffizienten ≥ 0,7: „sehr starker Einfluss des Prädiktors auf das Kriterium“
Anpassungsgüte (R2)
Ein Maß zur Bestimmung der Qualität der Anpassung ist die Anpassungsgüte R2, die oft auch als „Bestimmtheitsmaß“ bezeichnet wird. R2 hat einen Wertebereich zwischen 0 und 1. Üblich ist die Schreibweise in Prozent, also zwischen 0% und 100%. Man kann die Gesamtvarianz zerlegen, in die Varianz der vorhergesagten Werte des Mittelwertes und die sogenannte Rest- oder auch unerklärte Varianz vom beobachteten Wert zum vorhergesagten Wert. Die Anpassungsgüte gibt somit den Anteil des Kriteriums an, welcher durch die Varianz der Prädiktoren erklärt werden kann.
\color{black}{y_{i}=}\color{red}{a+b\cdot x_{i}}+\color{blue}{e_{i}}\color{black}{\frac{1}{N-1}\cdot\sum_{i=1}^N(y_{i}-\bar{y})^{2}=}\color{red}{\frac{1}{N-1}\cdot\sum_{i=1}^N(\hat{y_{i}}-\bar{y})^{2}}+\color{blue}{\frac{1}{N-1}\cdot\sum_{i=1}^N({y_{i}}-\hat{y_{i}})^{2}}\color{black}{s_Y^2=} \color{red}{s_{\hat{Y}}^2}+\color{blue}{s_e^2}\color{black}{s_Y^2}= Varianz der beobachteten Werte des Kriteriums Y
\color{red}{s_{\hat{Y}}^2}= Varianz der vorhergesagten Werte (ŷ),d.h.die durch X „erklärte“ Varianz
\color{blue}{s_e^2}= Restvarianz bzw.„unerklärte“ Varianz
Berechnet wird die Anpassungsgüte R2 aus dem Anteil der Varianz der vorhergesagten Werte (ŷ) an der Varianz der beobachteten Werte des Kriteriums Y.
R^{2}=\frac{s_{\hat{Y}}^2}{s_{Y}^2}Bei der einfachen linearen Regression darf angenommen werden:
R^{2}=\beta^{2}=r_{XY}^2Die Anpassungsgüte wird mit drei gültigen Stellen angegeben. Im Beispiel wäre zu formulieren: „Es lassen sich 54,6% der Varianz der Kommunikation durch die Zuneigung erklären.“
Signifikanztest des Regressionskoeffizienten b
Um zu prüfen, ob das empirische Regressionsgewicht b mit hinreichender Sicherheit aus einer Grundgesamtheit stammt, in der das wahre Regressionsgewicht gleich Null ist, wird der Signifikanztest des Regressionskoeffizienten b berechnet. Die Nullhypothese nimmt ein Regressionsgewicht gleich Null an.
Zweiseitiges Problem (einseitige Testung empfiehlt sich häufig):
H_{0}:b=0H_{1}:b\neq0Signifikanztest:
t=\frac{b}{SE_{b}}\qquad mit \qquad df=N-2SE_{b}(auch\,s_b\, Standartfehler\, des\, Regressionskoeffizienten)=\frac{s_{e}}{\sqrt{QS_{X}}}s_{e}=\sqrt{\frac{\sum_{i=1}^N e_i^2}{N-2}}QS_{X}=\sum_{i=1}^N(x_{i}-\bar{x})^2Testentscheidung nach festgelegtem Signifikanzniveau:
- Der kritische Wert tkrit kann unter Berücksichtigung des Signifikanzniveaus 𝛼 und der Freiheitsgrade df aus der t-Verteilungstabelle ausgelesen werden.
- H0 wird abgelehnt, wenn | t | > tkrit
Für das Beispiel ist:
SE_{b}=0,40t=\frac{b}{SE_{b}}=\frac{1,24}{0,40}=3,10 \qquad mit \qquad df=N-2=10-2=8Der kritische Wert bei 𝛼 = 0,05 für df = 8 lautet tkrit = 2,31.
Testentscheidung
Da | t | = 3,10 > tkrit wird H0 abgelehnt und H1 darf angenommen werden.
b) Multiple lineare Regression
Bei der multiplen linearen Regression wird das Kriterium (Y) auf zwei oder mehr Prädiktoren (X1 , X2 , …, Xk) zurückgeführt. Ziel ist das Auffinden einer Regressionsgeraden, die die (multidimensionale) Punktewolke möglichst gut abbildet. Die lineare Regressionsfunktion für k Prädiktoren lässt sich so darstellen:

Y=a+b_{1}\cdot X_{1}+b_{2}\cdot X_{2}+...+b_{k}\cdot X_{k}+eAnhand der k-Stück standardisierten Regressionskoeffizienten (𝛽, „Betas“) lässt sich beurteilen, welche Prädiktoren besser und welche schlechter für eine Vorhersage geeignet sind.
Gestufter Einschluss von Prädiktoren
Es werden zwei Methoden angewandt, um zu entscheiden, welche Prädiktoren für eine Vorhersage ausgeschlossen werden sollten.
Der hierarchische Einschluss von Prädiktoren ist – wenn theoretisch fundiert und theoriegeleitet – der Goldstandart. Dabei gehen einzelne Prädiktoren oder Blöcke von Prädiktoren in einer vorab definierten Reihenfolge in die Berechnung ein. So lässt sich prüfen, welche zusätzliche Erklärungskraft durch den Einschluss bestimmter Prädiktoren erzielt wird („Änderung in R2„).
Die zweite Methode ist der schrittweise Einschluss von Prädiktoren, die anhand statistischer Kriterien in die Regression aufgenommen oder entfernt werden, um die erklärte Varianz zu maximieren, jedoch wird dabei die Entscheidung über Inklusion bzw. Exklusion von Prädiktoren der Software überlassen.
Voraussetzungen für die lineare Regression
Für eine sinnvolle Interpretation müssen Voraussetzungen erfüllt sein:
- Die Variablen müssen metrisch skaliert sein.
- Die Variablen müssen normalverteilt sein.
- Der Zusammenhang zwischen den Variablen muss im ausgegebenen Streudiagramm linear erscheinen.
- Der Fehlerterm muss unabhängig sein. Der Durbin-Watson-Koeffizient sollte idealerweise 2 sein. Werte zwischen 1 und 3 lassen sich aber noch rechtfertigen.
- Multikollinearität muss ausgeschlossen werden. Die Diagnose sollte VIF-Werte kleiner 10 und eine Toleranz größer 0,1 ergeben. Nur dann darf eine Unabhängigkeit der Prädiktoren angenommen werden.
- Die Residuen für die einzelnen Beobachtungen müssen unkorreliert sein.
- Die Residuen müssen normalverteilt sein.
- Homoskedastizität der Residuen muss angenommen werden dürfen: Die Varianz der Residuen muss unabhängig von den x‐Werten sein.
- Alle relevanten Variablen müssen berücksichtigt werden.
- Ausreißer können die Schätzung stark verzerren und sollten, wenn möglich, ausgeschlossen werden.
Einfache lineare Regression in R
Die Funktion regress() aus dem tidycomm-Package berechnet den unstandardisierten Regressionskoeffizienten b und den standardisierten Regressionskoeffizienten 𝛽. Als Kriterium ist die zuerst genannte Variable definiert.
Dazu wird der Signifikanztest mit seinem t– und p-Wert durchgeführt und die Anpassungsgüte ausgegeben. Damit zusammenhängend wird eine Varianzanalyse mit einem F-Wert ausgegeben, um die Signifikanz des Gesamtmodells zu prüfen. Für den WoJ-Datensatz, für den Journalist:innen befragt wurden, lassen sich so Regressionen errechnen.
Befehl:
WoJ %>% regress(autonomy_selection, ethics_1)Ausgabe:
# A tibble: 2 × 6
Variable B StdErr beta t p
* <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 3.99 0.0481 NA 82.9 0
2 ethics_1 -0.0689 0.0259 -0.0766 -2.66 0.00798
# F(1, 1195) = 7.061023, p = 0.007983, R-square = 0.005874Es ist auch möglich eine lineare Modellierung mehrerer Prädiktoren durchzuführen. Hier wird die schrittweise Regressionsmodellierung verwendet:
Befehl:
WoJ %>% regress(ethics_1, autonomy_selection, work_experience)Ausgabe:
# A tibble: 3 × 6
Variable B StdErr beta t p
* <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 2.03 0.129 NA 15.8 5.32e-51
2 autonomy_selection -0.0692 0.0325 -0.0624 -2.13 3.32e- 2
3 work_experience -0.00762 0.00239 -0.0934 -3.19 1.46e- 3
# F(2, 1181) = 8.677001, p = 0.000182, R-square = 0.014482Dabei sollten gleich die Voraussetzungen für die lineare Regression (z. B. Multikollinearität und Homoskedastizität) überprüft werden. Dafür müssen optionale Argumente/Parameter angegeben werden.
Befehl:
WoJ %>% regress(ethics_1, autonomy_selection, work_experience,
check_independenterrors = TRUE, #Durbin-Watson-Tests
check_multicollinearity = TRUE, #Variance Inflation Factor (VIF) und Toleranz (1/VIF)
check_homoscedasticity = TRUE #Breusch-Pagan-Tests
) Ausgabe:
# A tibble: 3 × 8
Variable B StdErr beta t p VIF tolerance
* <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 2.03 0.129 NA 15.8 5.32e-51 NA NA
2 autonomy_select… -0.0692 0.0325 -0.0624 -2.13 3.32e- 2 1.03 0.974
3 work_experience -0.00762 0.00239 -0.0934 -3.19 1.46e- 3 1.03 0.974
# F(2, 1181) = 8.677001, p = 0.000182, R-square = 0.014482
- Check for independent errors: Durbin-Watson = 2.037690 (p = 0.490000)
- Check for homoscedasticity: Breusch-Pagan = 6.966472 (p = 0.008305)
- Check for multicollinearity: VIF/tolerance added to outputVisualisierung von Regressionen in R
Mit der visualize()-Funktion lassen sich die Regressionen graphisch darstellen. Für Hilfe bei der Interpretation der Regressionsdiagramme kann man den Hilfebefehl ?visualize() eingeben und nach unten scrollen, bis man zu regress() gelangt. Für Fragen zur regress()-Funktion kann man den Hilfebefehl ?regress() nutzen.
1. Basis-Visualisierung:
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize()Ausgabe:
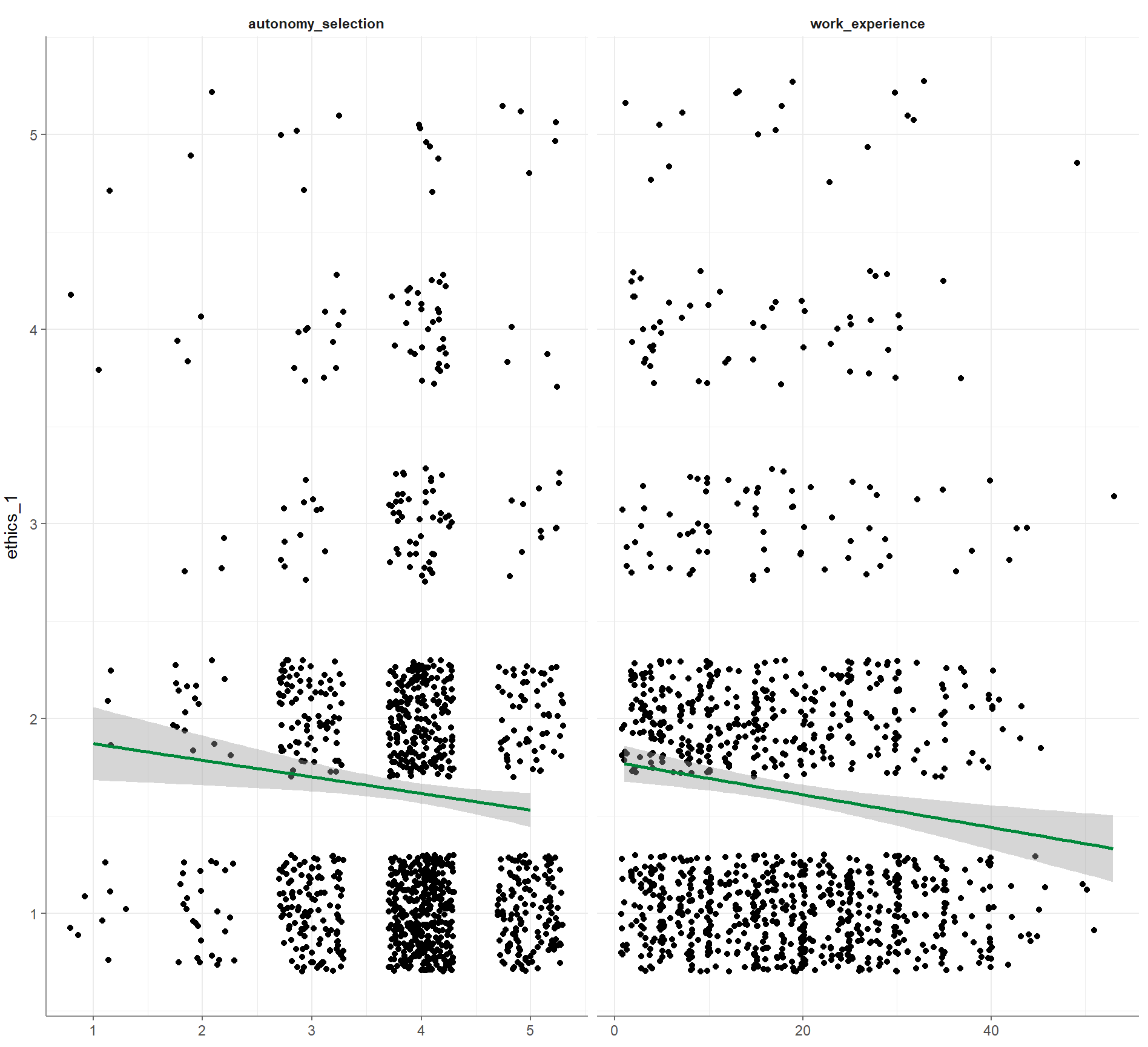
2. Korrelogramm der Prädiktoren:
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize(which = "correlogram")Ausgabe:
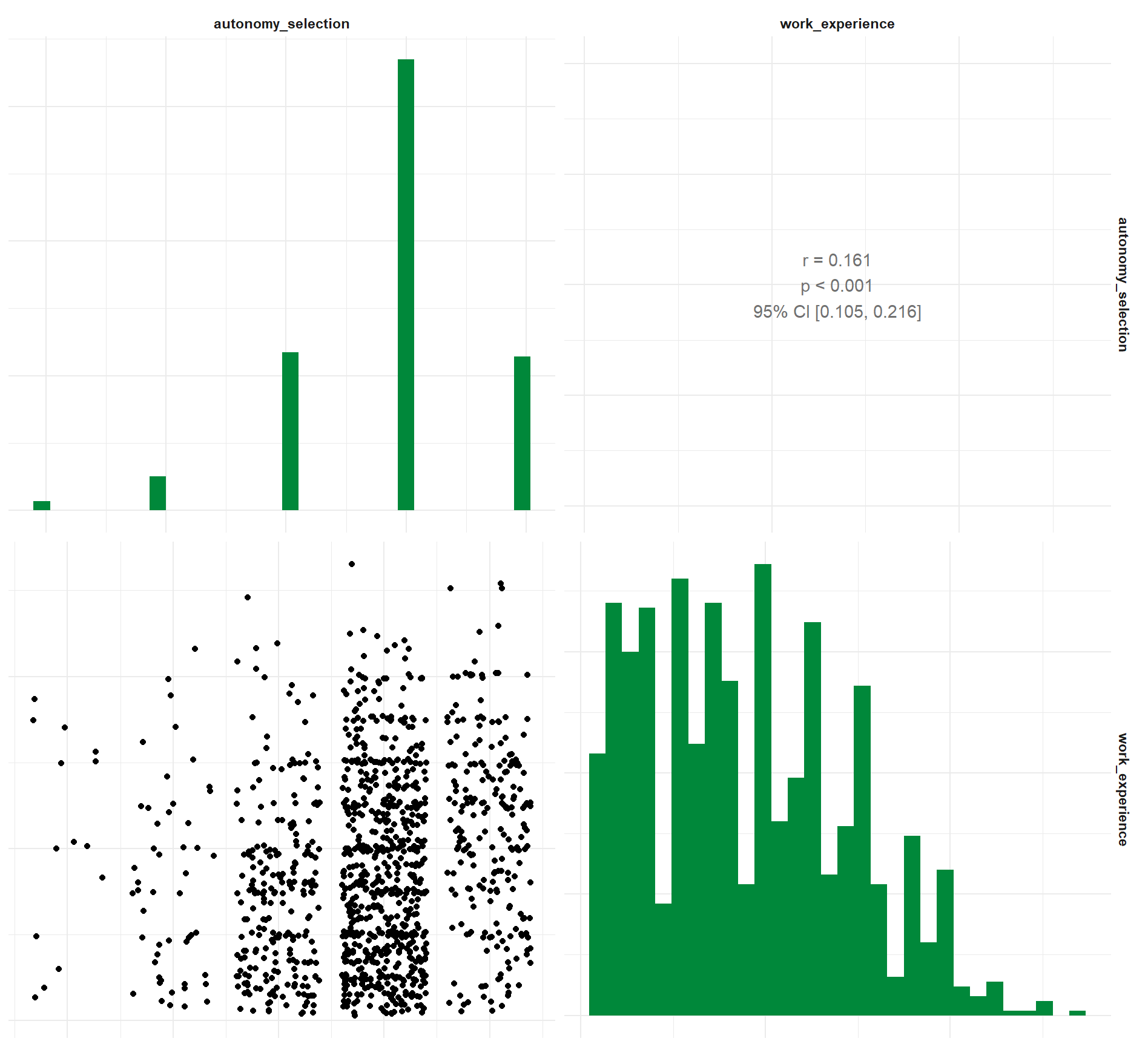
3. Residuals-versus-fitted plot zur Bestimmung von deren Verteilungen:
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize(which = "resfit")Ausgabe:
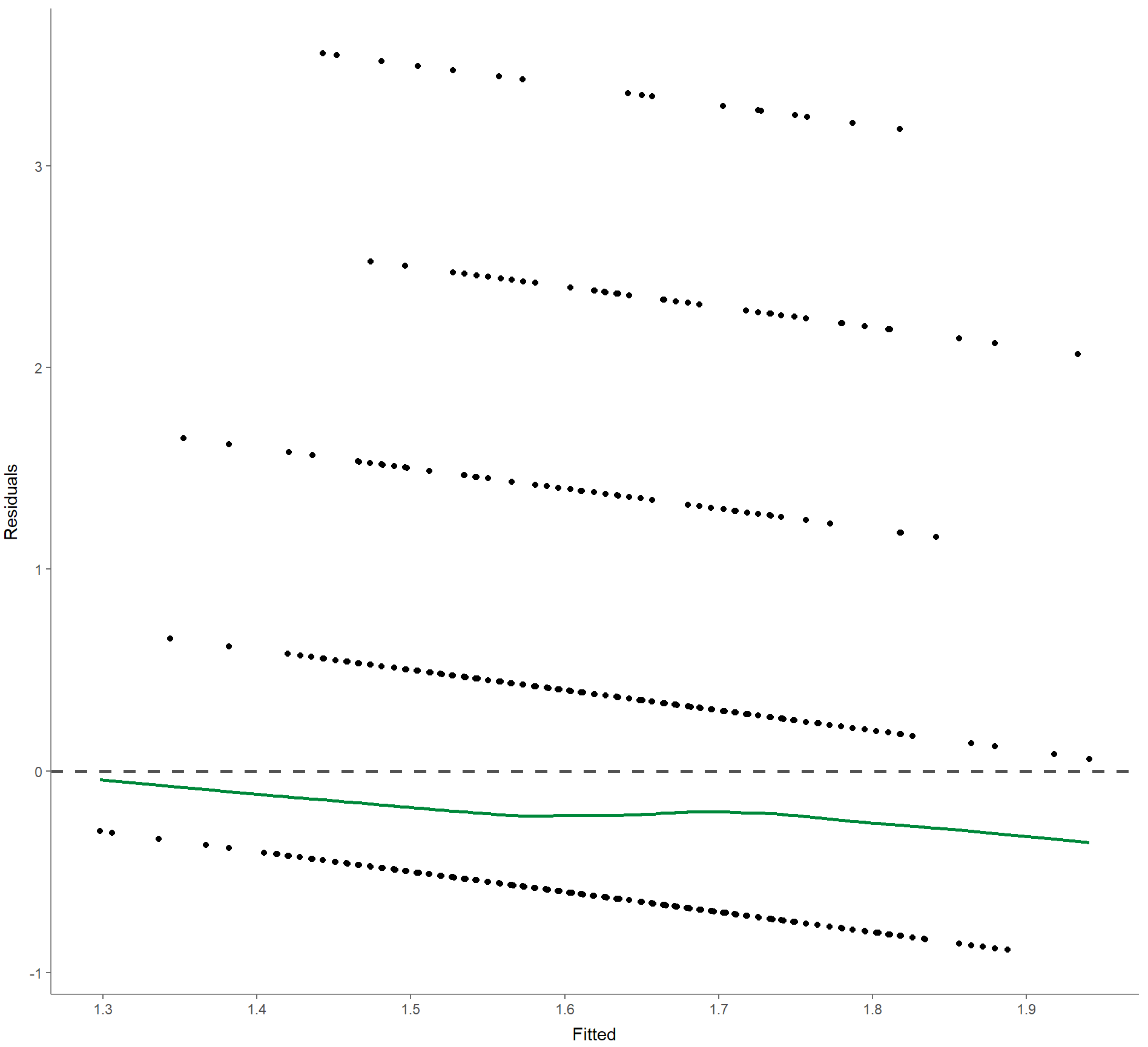
4. Normales Wahrscheinlichkeits-Diagramm zur Überprüfung auf Multikollinearität:
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize(which = "pp")Ausgabe:
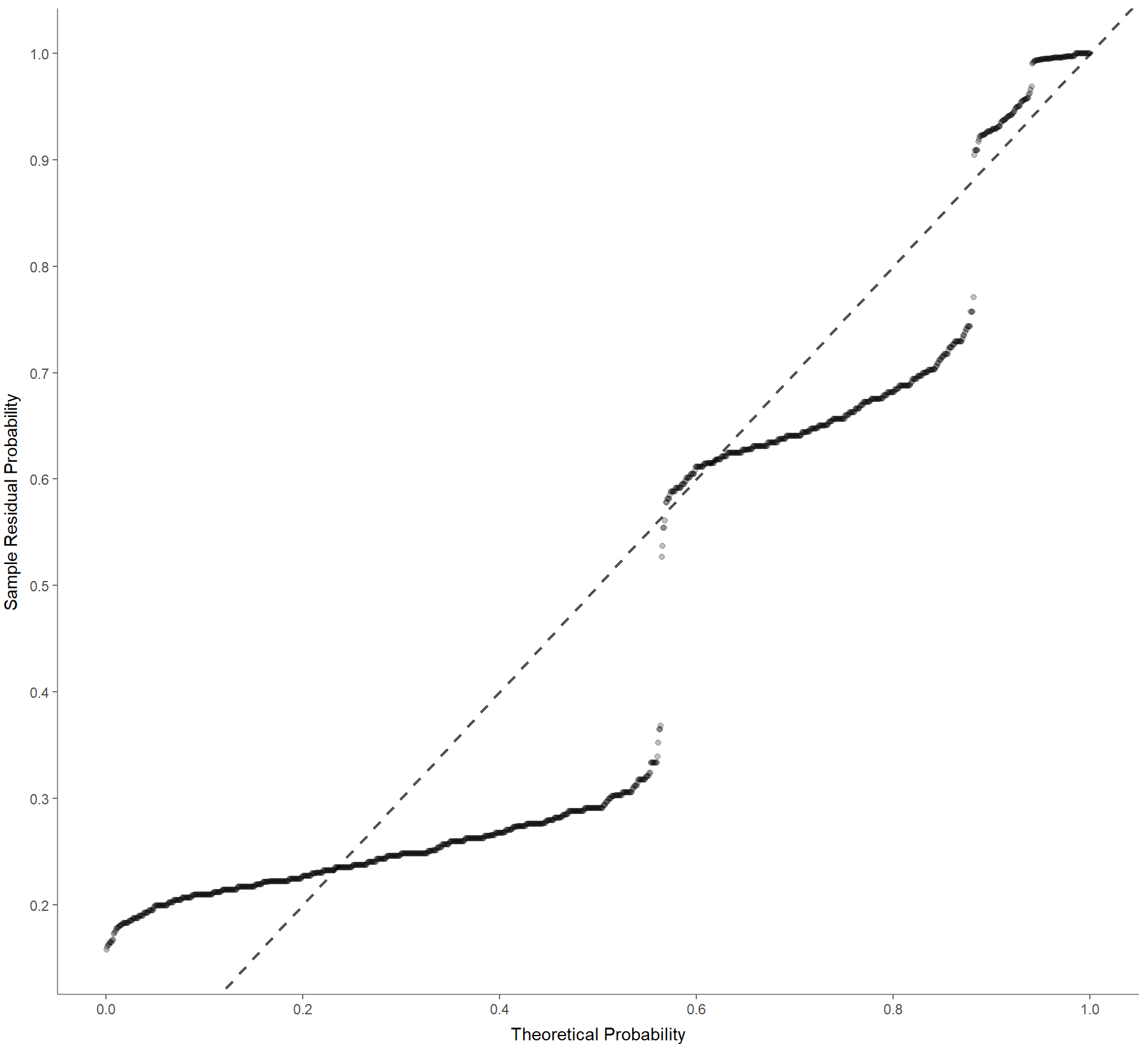
5. Scale-location (manchmal auch spread-location/Streuungslage genannt), um zu prüfen, ob die Residuen gleichmäßig verteilt sind (um die Homoskedastizität zu prüfen):
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize(which = "scaloc")Ausgabe:
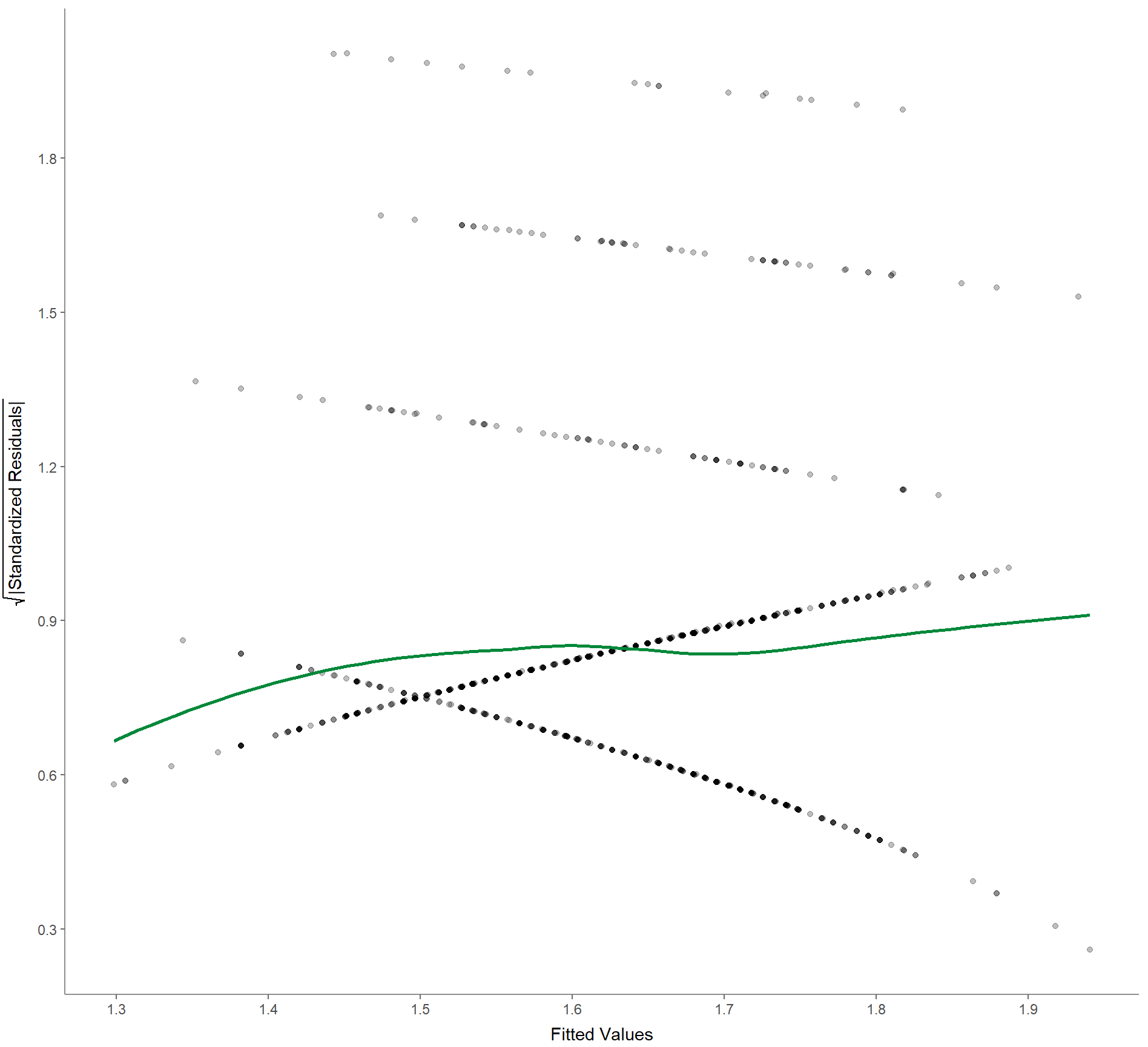
6. Residuen-gegen-Mittelwert-Diagramm zur Überprüfung auf einflussreiche Ausreißer, die das endgültige Modell stärker beeinflussen als den Rest der Daten:
Befehl:
WoJ %>%
regress(ethics_1, autonomy_selection, work_experience) %>%
visualize(which = "reslev")Ausgabe:
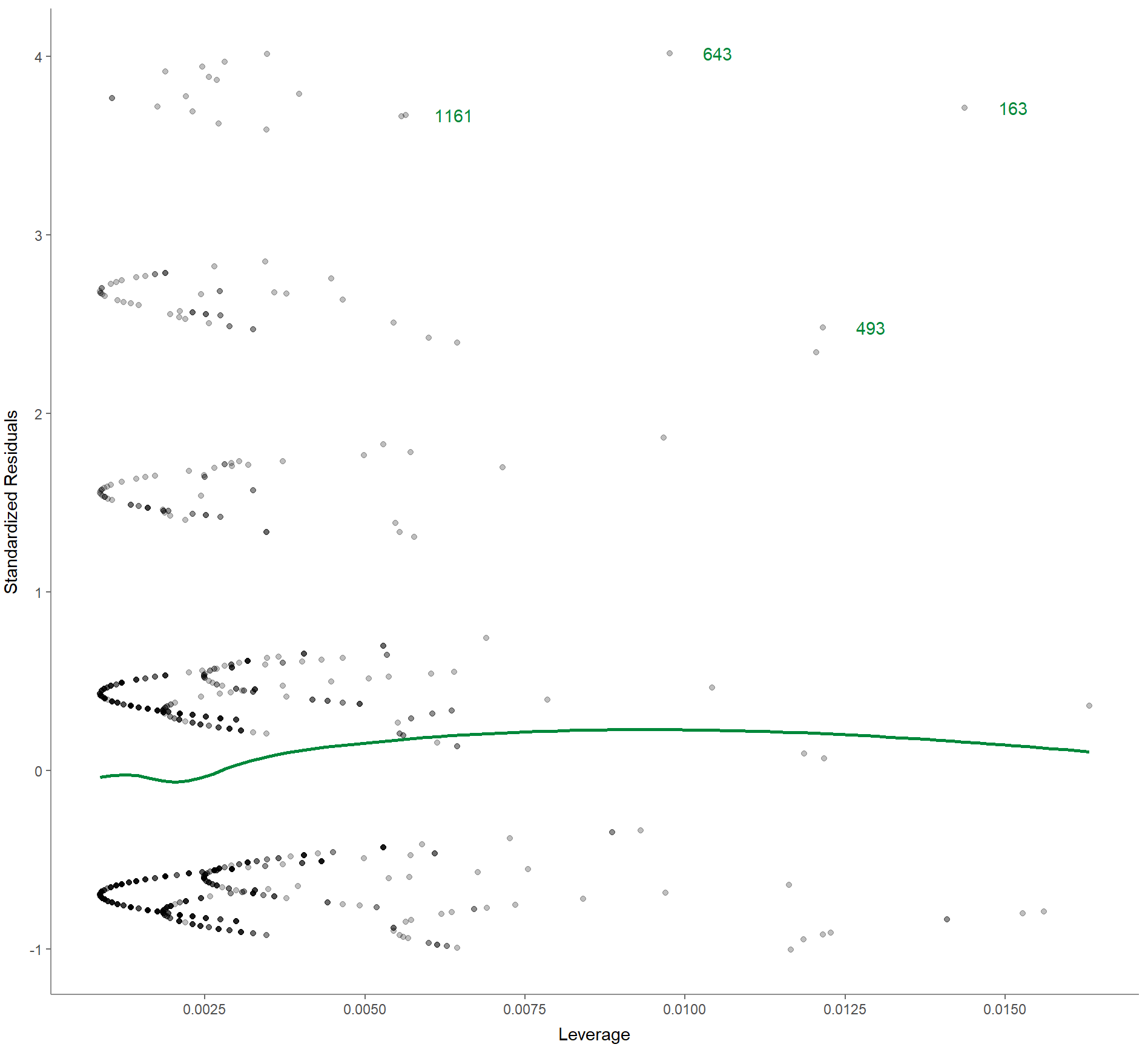
Korrelationen berichten
Notwendige Informationen
- Stichprobengröße
- Stärke des Einflusses
- Richtung des Einflusses bzw. Vorzeichen der Regressionskoeffizienten
- Signifikanz und jeweiliges Signifikanzniveau des Einflusses mit t– und p-Wert
- Informationen zur Stichprobengröße (N oder df)
- Anpassungsgüte
- Kontextualisierung von b: Um wie viel verändert sich das Kriterium, wenn der Prädiktor um eine Zähleinheit erhöht wird.
- Einseitige oder zweiseitige Testung
Beispielbericht
„Wir können auch bei einseitiger Testung nicht annehmen, dass der Prädiktor Zustimmung zur Aussage „Journalisten sollten sich unabhängig von der Situation und dem Kontext immer an berufsethische Regeln halten“ das Kriterium der wahrgenommenen Autonomie bei der Auswahl von Nachrichten beeinflusst. Der Einfluss ist zwar statistisch signifikant, jedoch zu gering. Nur etwa 0,6% der Varianz des Kriteriums lassen sich auf den Prädiktor zurückführen (df = 1195; b = -0,069; 𝛽 = -,076; t = -2.66; p < ,010; R2 = ,006).“
