Skalenniveaus

Lehrvideo

Was sind Skalen?

Skalen sind Werkzeuge in der Statistik, mit denen Merkmale von Objekten oder Lebewesen gemessen und kategorisiert werden. Sie dienen dazu, die Daten in einer strukturierten und quantifizierbaren Form darzustellen, sodass sie analysiert und interpretiert werden können. Skalen ermöglichen es Forscher*innen und Datenanalyst*innen, empirische Daten zu sammeln und auf dieser Basis wissenschaftliche Hypothesen zu testen.

Die Verwendung der „richtigen“ Skala ist im Forschungsprozess entscheidend, weil sie bestimmt, welche statistischen Methoden angewendet werden können und wie die Ergebnisse interpretiert werden müssen. Daher ist es wichtig, ein tiefes Verständnis für die verschiedenen Arten von Skalenniveaus zu haben, welche in der Statistik typischerweise verwendet werden: Nominal-, Ordinal-, Intervall- und Verhältnisskala.

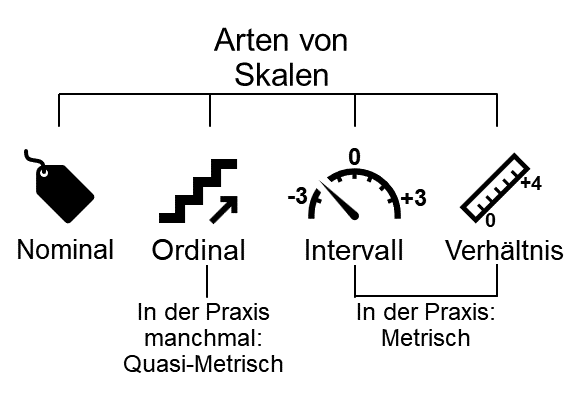
Arten von Skalen

Nominalskala

Die Nominalskala ist das einfachste Skalenniveau. Daten auf diesem Niveau werden in Kategorien eingeteilt, die sich gegenseitig ausschließen. Ein typisches Beispiel sind Geschlechter oder Nationalitäten. Wichtig ist:

1. Vergleichbarkeit: Nur Gleichheit und Ungleichheit von Daten können festgestellt werden.
2. Rechenoperationen: Keine mathematischen Operationen (außer Zählen) sind zulässig.
3. Beispiel: Geschlecht (männlich, weiblich, divers).

Ordinalskala

Daten auf der Ordinalskala sind geordnet. Das bedeutet, dass neben der bloßen Kategorisierung auch eine Rangordnung existiert, d.h., man kann die Kategorien also in eine sachlogische Reihenfolge bringen. Allerdings gibt der Abstand zwischen den Rängen keine quantitativ messbare Information. Beispiele hierfür sind Bildungsniveaus oder Schulnoten.

1. Vergleichbarkeit: Rangordnung ist möglich.
2. Rechenoperationen: Median und Modus können berechnet werden, Mittelwert und Standardabweichung jedoch nicht.
3. Beispiel: Schulnoten (1, 2, 3, 4, 5, 6) oder Bildungsniveaus („hoch gebildet“, „durchschnittlich gebildet“, „niedrig gebildet“)

Intervallskala

Bei der Intervallskala sind nicht nur die Ränge geordnet, sondern auch die Abstände zwischen den Skalenpunkten gleich und sinnvoll interpretierbar. Es gibt jedoch keinen absoluten Nullpunkt. Ein klassisches Beispiel ist die Temperaturmessung in Celsius oder Fahrenheit.

1. Vergleichbarkeit: Unterschiede zwischen Datenpunkten sind quantitativ auswertbar.
2. Rechenoperationen: Addition und Subtraktion sind möglich, ebenso die Berechnung von Mittelwert und Standardabweichung.
3. Beispiel: Temperatur in Celsius.

Verhältnis- oder Ratioskala

Die Verhältnis- oder Ratioskala ist das höchste Skalenniveau. Sie umfasst alle Eigenschaften der Intervallskala, besitzt aber zusätzlich einen absoluten Nullpunkt, der das Fehlen der gemessenen Größe anzeigt. Dies ermöglicht alle mathematischen Operationen.

1. Vergleichbarkeit: Verhältnisse zwischen den Messwerten sind aussagekräftig.
2. Rechenoperationen: Addition, Subtraktion, Multiplikation und Division sowie die Berechnung von Mittelwert und Standardabweichung.
3. Beispiel: Gewicht in Kilogramm, Alter in Jahren oder Temperatur in Kelvin.

Erklärung: Warum ist die Temperatur in Celsius und Fahrenheit intervallskaliert, aber die Temperatur in Kelvin verhältnisskaliert? Kelvin hat einen absoluten Nullpunkt (0 K), der den Punkt darstellt, an dem keine kinetische Energie mehr in den Atomen vorhanden ist – theoretisch die niedrigstmögliche Temperatur der Welt (nicht einmal der Weltraum ist so kalt!). Dieser Nullpunkt ist nicht willkürlich, sondern physikalisch begründet. Dadurch, dass Kelvin einen absoluten Nullpunkt hat, ermöglicht die Skala es, Verhältnisse zwischen absoluten Temperaturen anzugeben. Zum Beispiel bedeutet 200 K das Doppelte der kinetischen Energie von 100 K.

Celsius und Fahrenheit haben dagegen keinen natürlichen Nullpunkt, weil ihre Nullpunkte willkürlich festgelegt sind und nicht das vollständige Fehlen der gemessenen physikalischen Größe, wie etwa thermische Energie, darstellen. Bei der Celsius-Skala entspricht der Nullpunkt dem Gefrierpunkt von Wasser bei einem bestimmten Druck (1 atm), also 0 °C (= 273,15 K). Dieser Punkt wurde aus praktischen Gründen gewählt, weil Wasser ein häufiges und leicht verfügbares Material ist, das Phasen wechselt (z.B. von flüssig zu gefroren). Ähnlich ist es bei der Fahrenheit-Skala, deren Nullpunkt bei 0 °F (= 255,37 K) nach einer älteren Definition der kälteste Temperaturpunkt war, den der Erfinder Daniel Fahrenheit in seiner Umgebung (mit einer Mischung aus Eis, Wasser und Ammoniumchlorid) reproduzieren konnte.

Skalen in der Praxis

Metrische Skala

In der statistischen Praxis wird oft der Begriff „metrische Skala“ verwendet, um Skalen zu beschreiben, die entweder auf der Intervall- oder der Verhältnisskala gemessen wurden. Die Verwendung des allgemeineren Begriffs „metrische Skala“ in der Praxis ist ein Kompromiss zwischen theoretischer Genauigkeit und praktischer Anwendbarkeit, weil die Unterscheidung zwischen Intervall- und Verhältnisskalen in vielen praktischen Anwendungen nicht kritisch ist. Sowohl Intervall- als auch Verhältnisskalen ermöglichen die Verwendung von Addition und Subtraktion sowie die Berechnung von Mittelwerten und Standardabweichungen. In vielen praktischen Fällen, besonders in der Sozialforschung, sind diese Operationen ausreichend, um die notwendigen statistischen Analysen durchzuführen.

Quasi-Metrische Skala

Quasi-metrische Skalen sind Skalen, die in der Praxis oft wie metrische Skalen behandelt werden, obwohl sie streng genommen nicht alle Kriterien dafür erfüllen. Das passiert häufig bei ordinalen Skalen, die durch die Erhebungsmethode oder Datenverarbeitung numerische Werte erhalten, welche dann so behandelt werden, als wären sie metrisch.

Beispiele für quasi-metrische Skalen:

1. Schulnoten: Obwohl Schulnoten (1 bis 6) eine klare Rangordnung haben, sind die Abstände zwischen den Noten nicht notwendigerweise gleich oder messbar. Dennoch werden sie oft in statistischen Analysen als quasi-metrisch behandelt, indem man z.B. den Notendurchschnitt berechnet.
2. Likert-Skalen in Umfragen: Antworten auf einer Likert-Skala (z.B. von 1 „stimme gar nicht zu“ bis 5 „stimme voll zu“) sind streng genommen ordinal, aber in der Praxis werden sie häufig summiert oder gemittelt, was sie quasi-metrisch macht.