t-Test für unabhängige Stichproben

Der t-Test für unabhängige Stichproben prüft, ob sich die Mittelwerte x̄₁ und x̄₂, zweier unabhängiger Stichproben, systematisch voneinander unterscheiden. Statistisch prüft er, ob die zwei Stichproben aus Grundgesamtheiten stammen, deren Parameter μ₁ und μ₂ identisch sind. Der t-Test für unabhängige Stichproben wird auch als two-sample t-Test, doppelter t-Test oder Zweistichproben-t-Test bezeichnet.

Voraussetzungen des t-Tests für unabhängige Stichproben

• Die Daten der Stichprobe entstammen zwei normalverteilten Grundgesamtheiten. Dafür ist nach dem zentralen Grenzwertsatz ein Stichprobenumfang von jeweils größer 30 hinreichend.
• Beide Stichproben müssen Grundgesamtheiten entstammen, die unabhängig voneinander sind.
• Die Abhängige Variable ist (quasi-)metrisch skaliert.
• Beide Stichproben müssen die gleiche bzw. sehr ähnliche Varianz haben. Die Varianzhomogenität wird mit dem Levene-Test ermittelt. Ist der Test signifikant (d.h. p < ,050), unterscheiden sich die Varianzen der beiden Stichproben und es muss eine Korrektur der Freiheitsgrade vorgenommen werden. Bei Verletzung der Voraussetzung der Varianzhomogenität kann der Welch-Test gerechnet werden.

Signifikanztest des t-Tests für unabhängige Stichproben

Um zu prüfen, ob sich die Mittelwerte mit hinreichender Sicherheit voneinander unterscheiden, wird der Signifikanztest des t-Tests für unabhängige Stichproben gerechnet.

Einseitiges Problem:

H_{0}:\mu_{1}\leq \mu_{2}\qquad oder \qquad \mu_{1}\geq \mu_{2}\ 

H_{1}: \mu_{1}> \mu_{2}\qquad oder \qquad \mu_{1}< \mu_{2}\ 

Zweiseitiges Problem:

H_{0}: \mu_{1}=\mu_{2}

H_{1}: \mu_{1}\neq\mu_{2} 

Signifikanztest:

Die gepolte Streuung für zwei gleich große Stichproben n₁ = n₂ berechnet sich aus den Varianzen der Stichproben:

s_p^2=\frac{s_1^2+s_2^2}{2}

Die gepolte Streuung für zwei ungleich große Stichproben n₁ ≠ n₂ berechnet sich aus den Varianzen der Stichproben:

s_p^2=\frac{(n_{1}-1)\cdot s_1^2+(n_{2}-1)\cdot s_2^2}{n_{1}+n_{2}-2}

Die durchschnittliche Abweichung des geschätzten Mittelwertunterschieds vom tatsächlichen Mittelwertunterschied wird als Standardfehler der Mittelwertdifferenz bezeichnet und errechnet sich aus der gepolten Streuung und Fallzahl.

SE_{(\bar{x}_1-\bar{x}_2)}=\sqrt{s_p^2\cdot (\frac{1}{n_{1}}+\frac{1}{n_{2}})}

Der kritische t-Wert t_krit ist dann:

t=\frac{\bar{x}_1-\bar{x}_2}{SE_{(\bar{x}_1-\bar{x}_2)}}\qquad mit \qquad df=n_{1}+n_{2}-2

Testentscheidung nach festgelegtem Signifikanzniveau:

• Der kritische Wert t_krit kann unter Berücksichtigung des Signifikanzniveaus 𝛼 und der Freiheitsgrade df aus der t-Verteilungstabelle ausgelesen werden.
• Wird einseitig getestet entspricht der kritische Wert dem (1-α)-Quantil der t-Verteilung. Wird zweiseitig getestet entspricht der kritische Wert dem (1-α/2)-Quantil der t-Verteilung. Der zweiseitige Test ist also konservativer.
• H₀ wird abgelehnt, wenn | t | > t_krit.

Effektstärke

Die Effektstärke gibt an, wie stark der Effekt der Gruppenzugehörigkeit auf die abhängige Variable ist. Nur wenn die Mittelwertdifferenz signifikant ist, findet eine Berechnung der Effektstärke statt.

Cohens d

Als standardisiertes Maß für die Effektstärke kann Cohens d genutzt werden, das die Distanz zwischen Populationsmittelwerten angibt:

d=\frac{{\bar{x}_1-\bar{x}_2}}{\sqrt{s_p^2}}=\frac{{\bar{x}_1-\bar{x}_2}}{s_p}

Interpretationskonvention nach Cohen (1988):

• Betrag von Cohens d < 0,2: „kein Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Cohens d ≥ 0,2: „geringer Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Cohens d ≥ 0,5: „mittlerer Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Cohens d ≥ 0,8: „starker Effekt der unabhängigen Variable auf die abhängige Variable“

Varianzquotient η²

Der Varianzquotient η² (sprich: Eta Quadrat) gibt an, welcher Anteil der Varianz, der abhängigen Variable auf die Varianz der unabhängigen Variable zurückgeführt werden kann.

Dafür wird zuerst der Populationseffekt geschätzt:

f_s^2=\frac{t^2}{df}

Damit lässt sich die Varianzaufklärung errechnen:

\eta^2=\frac{f_s^2}{1+f_s^2}

η² wird im Forschungsbericht in Prozent angegeben.

Verwendete Kürzel

• n₁ (n₂): Größe der Teilstichprobe 1 (2)
• x̄₁ (x̄₂): Mittelwerte der Teilstichprobe 1 (2)
• s₁ (s₂): Standardabweichungen der Teilstichprobe 1 (2)
• s_p²: gepolte Streuung
• SE_{(x̄1 – x̄2)}: Standardfehler der Mittelwertdifferenz
• d: Cohens d
• f_s²: Schätzung des Populationseffekts
• η²: Varianzaufklärung Eta Quadrat

t-Test für unabhängige Stichproben in R

Zweiseitiger Test

Die Funktion t_test() aus dem tidycomm-Package berechnet unter anderem t-Tests für unabhängige Stichproben. Die t_test()-Funktion gibt, getrennt nach den zwei Teilstichproben, in einer Tabelle die Stichprobenmittelwerte und Standartabweichungen an. Es wird der Name der abhängigen Variable, die Mittelwertdifferenz, der kritische t-Wert t_krit, die jeweiligen Freiheitsgrade und der p-Wert ausgegeben. Zusätzlich wird Cohens d und der Levene-Test berechnet. Ist der Levene-Test signifikant liegt keine Varianzhomogenität vor. Die t_test()-Funktion rechnet dann automatisch den Welch-Test, der robust gegenüber Heteroskedastizität ist.

Mit dem WoJ-Datensatz und der t_test()-Funktion kann überprüft werden, ob sich unbefristet und befristet beschäftigte Journalist:innen mit hinreichender Sicherheit im Hinblick auf die Wahrnehmung ihrer Autonomie unterscheiden (zweiseitiger t-Test). Die Alternativhypothese lautet demnach, dass der Mittelwertunterschied zwischen unbefristet und befristet beschäftigten Journalist:innen ungleich Null ist.

Zunächst wird mit der describe()-Funktion aus dem tidycomm-Package und der group_by-Funktion aus dem dplyr-Package ermittelt, ob alle Voraussetzungen erfüllt sind.

Befehl:

WoJ %>%
  dplyr::group_by(temp_contract) %>%
  describe(autonomy_emphasis)

Ausgabe:

> WoJ %>%
+   dplyr::group_by(temp_contract) %>%
+   describe(autonomy_emphasis)
# A tibble: 3 × 16
# Groups:   temp_contract [3]
  temp_contract Variable              N Missing     M    SD   Min   Q25   Mdn   Q75   Max Range CI_95_LL CI_95_UL Skewness Kurtosis
* <fct>         <chr>             <int>   <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
1 Permanent     autonomy_emphasis   944       4  4.12 0.768     1     4     4     5     5     4     4.07     4.17   -0.917     4.52
2 Temporary     autonomy_emphasis    53       0  3.89 0.870     2     3     4     4     5     3     3.65     4.13   -0.489     2.66
3 NA            autonomy_emphasis   198       1  3.90 0.855     1     4     4     4     5     4     3.78     4.02   -0.881     4.10

Nachdem beide Teilstichproben größer 30 sind, darf nach dem zentralen Grenzwertsatz eine Normalverteilung der Grundgesamtheiten angenommen werden. Die abhängige Variable Autonomie bei der Entscheidung, welche Aspekte einer Geschichte hervorgehoben werden (autonomy_emphasis) ist quasi-metrisch angegeben (1: „no freedom at all“ bis 5: „complete freedom“), die Gruppierungsvariable des Beschäftigungsverhältnisses (temp_contract) dichotom (Permanent oder Temporary) . Somit darf der t-Test für unabhängige Stichproben gerechnet werden.

Befehl:

WoJ %>% t_test(temp_contract, autonomy_emphasis)

Ausgabe:

> WoJ %>% t_test(temp_contract, autonomy_emphasis)
# A tibble: 1 × 12
  Variable          M_Permanent SD_Permanent M_Temporary SD_Temporary   Delta_M         t    df         p         d Levene_p var_equal
* <chr>               <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.3!> <num:.3!> <dbl> <num:.3!> <num:.3!>    <dbl> <chr>    
1 autonomy_emphasis       4.124        0.768       3.887        0.870     0.237     2.171   995     0.030     0.306    0.277 TRUE 

Der Levene-Test ist nicht signifikant, beide Stichproben haben die gleiche Varianz.

Erinnerung: Man kann die Analyse jederzeit in einem R-Objekt speichern und mit dem View()-Befehl überprüfen, um alle Spalten der Analyse zu sehen.

Befehl:

model1 <- WoJ %>% t_test(temp_contract, autonomy_emphasis)
  View(model1)

Ausgabe:

Einseitiger Test

Sie können anhand des Outputs des zweiseitigen t-Tests auch das Ergebnis des einseitigen t-Tests berechnen. So können Sie die Hypothese testen, dass unbefristet beschäftigte Journalist:innen mit hinreichender Sicherheit mehr Autonomie bei der Entscheidung empfinden, welche Aspekte einer Geschichte hervorgehoben werden, als ihre befristet beschäftigten Kolleg:innen (einseitiger t-Test). Die Alternativhypothese lautet demnach, dass der Mittelwertunterschied zwischen unbefristet und befristet beschäftigten Journalist:innen größer als Null ist.

Da der Autonomie-Mittelwert der unbefristet beschäftigten Journalist*innen tatsächlich annahmekonform höher ist (M = 4,12) als der ihrer befristet beschäftigten Kolleg*innen (M = 3,89), entspricht der p-Wert dieses einseitigen Tests dem halbierten Ergebnis des zweiseitigen Tests, d. h. p = ,030 : 2 = ,015.

t-Test für mehrere Variablen

Es ist auch möglich mehrere abhängige Variablen zu testen. Dafür werden diese Variablen ergänzt.

Befehl:

WoJ %>% t_test(temp_contract, autonomy_emphasis, autonomy_selection)

Ausgabe:

> WoJ %>% t_test(temp_contract, autonomy_emphasis, autonomy_selection)
The significant result from Levene's test suggests unequal variances among the groups, violating standard t-test assumptions. This necessitates the use of Welch's t-test, which is robust against heteroscedasticity.
# A tibble: 2 × 12
  Variable           M_Permanent SD_Permanent M_Temporary SD_Temporary   Delta_M         t    df         p         d Levene_p var_equal
* <chr>                <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.3!> <num:.3!> <dbl> <num:.3!> <num:.3!>    <dbl> <chr>    
1 autonomy_emphasis        4.124        0.768       3.887        0.870     0.237     2.171   995     0.030     0.306    0.277 FALSE    
2 autonomy_selection       3.910        0.755       3.698        0.932     0.212     1.627    56     0.109     0.277    0.043 FALSE  

Wird keine abhängige Variable angegeben, dann testet die t_test()-Funktion alle metrischen Variablen im Datensatz.

Befehl:

WoJ %>% t_test(temp_contract)

Ausgabe:

> WoJ %>% t_test(temp_contract)
# A tibble: 11 × 12
   Variable           M_Permanent SD_Permanent M_Temporary SD_Temporary   Delta_M         t    df         p         d Levene_p var_equal
 * <chr>                <num:.3!>    <num:.3!>   <num:.3!>    <num:.3!> <num:.3!> <num:.3!> <dbl> <num:.3!> <num:.3!>    <dbl> <chr>    
 1 autonomy_selection       3.910        0.755       3.698        0.932     0.212     1.627    56     0.109     0.277    0.043 TRUE     
 2 autonomy_emphasis        4.124        0.768       3.887        0.870     0.237     2.171   995     0.030     0.306    0.277 TRUE     
 3 ethics_1                 1.568        0.850       1.981        0.990    -0.414    -3.415   999     0.001    -0.482    0.644 TRUE     
 4 ethics_2                 3.241        1.263       3.509        1.234    -0.269    -1.510   999     0.131    -0.213    0.697 TRUE     
 5 ethics_3                 2.369        1.121       2.283        0.928     0.086     0.549   999     0.583     0.077    0.126 TRUE     
 6 ethics_4                 2.534        1.239       2.566        1.217    -0.032    -0.185   999     0.853    -0.026    0.791 TRUE     
 7 work_experience         17.707       10.540      11.283       11.821     6.424     4.288   989     0.000     0.605    0.857 TRUE     
 8 trust_parliament         3.073        0.797       3.019        0.772     0.054     0.480   999     0.631     0.068    0.683 TRUE     
 9 trust_government         2.870        0.847       2.642        0.811     0.229     1.918   999     0.055     0.271    0.724 TRUE     
10 trust_parties            2.430        0.724       2.358        0.736     0.072     0.703   999     0.482     0.099    0.62  TRUE     
11 trust_politicians        2.533        0.707       2.396        0.689     0.136     1.369   999     0.171     0.193    0.853 TRUE 

Es ist über das optionale Argument levels auch möglich nur zwei Ausprägungen von mehrstufigen unabhängigen Variablen einzubeziehen. Die Variable Beschäftigung (employment) liegt dreistufig vor (Freelancer, Full-Time und Part-Time). Im untenstehenden Beispiel werden nur die beiden Gruppen Full-Time versus Freelancer betrachtet.

Befehl:

WoJ %>% t_test(employment, 
               autonomy_emphasis, 
               levels = c("Full-time", "Freelancer")
              )

Ausgabe:

> WoJ %>% t_test(employment, 
+                autonomy_emphasis, 
+                levels = c("Full-time", "Freelancer")
+               )
# A tibble: 1 × 12
  Variable          `M_Full-time` `SD_Full-time` M_Freelancer SD_Freelancer   Delta_M         t    df         p         d Levene_p var_equal
* <chr>                 <num:.3!>      <num:.3!>    <num:.3!>     <num:.3!> <num:.3!> <num:.3!> <dbl> <num:.3!> <num:.3!>    <dbl> <chr>    
1 autonomy_emphasis         4.118          0.781        3.901         0.852     0.217     3.287  1067     0.001     0.274    0.175 TRUE  

Visualisieren von t-Tests für unabhängige Stichproben

Eine Visualisierung ist über die Funktion visualize() möglich:

Befehl:

WoJ %>% t_test(temp_contract, autonomy_emphasis) %>%
  visualize()

Ausgabe:

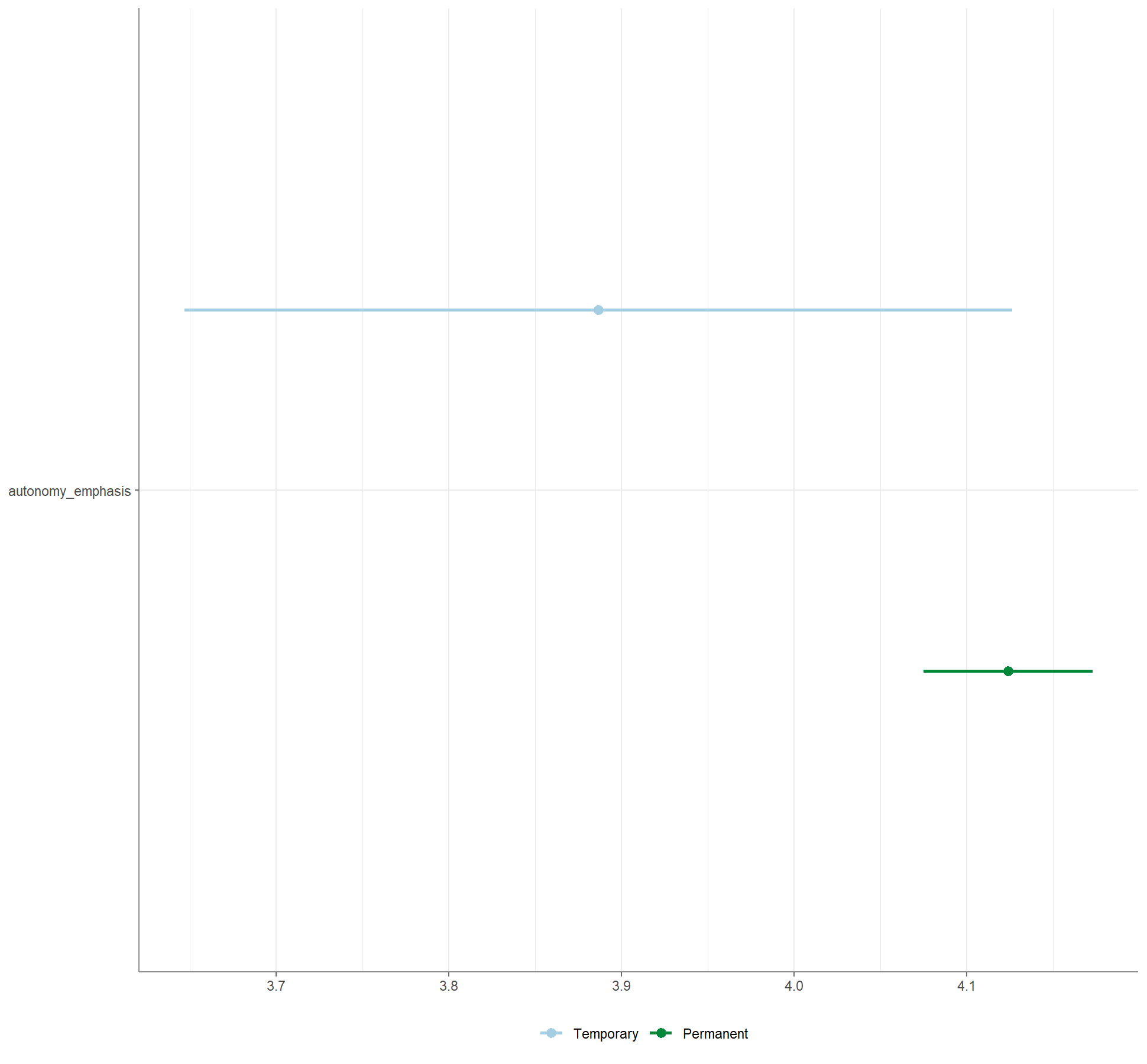
t-Tests für unabhängige Stichproben berichten

Notwendige Informationen

• Größe der Teilstichproben 1 (2): n₁ (n₂)
• Mittelwerte der Teilstichproben 1 (2): M₁ (M₂)
• Standardabweichungen der Teilstichproben 1 (2): SD₁ (SD₂)
• Kritischer t-Wert t_krit mit den Freiheitsgraden df
• Signifikanz und jeweiliges Signifikanzniveau des Zusammenhangs
• Cohens d
• Varianzaufklärung η² (nicht zwingend)

Beispielbericht

„Unbefristet beschäftigte Journalist:innen nehmen eine signifikant höhere Autonomie bei der Entscheidung wahr, welche Aspekte einer Geschichte hervorgehoben werden, als ihre befristet beschäftigte Kolleg:innen. Das Beschäftigungsverhältnis erklärt 0,5% der empirischen Varianz der Autonomiewahrnehmung und hat einen geringen Effekt (n_Permanent = 944; M_Permanent = 4,12; SD_Permanent = 0,768; n_Temporary = 53; M_Temporary = 3,89; SD_Temporary = 0,87; t(995) = 2,171; p = ,030; d = ,31; η² = ,005).“

Referenzen

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2. Ausgabe). Routledge. https://doi.org/10.4324/9780203771587