Was ist ein z-Test?
Der z-Test ist ein Hypothesentest, der Hypothesen über die Häufigkeit von einem Merkmal in der Grundgesamtheit testet. Er stellt ein Werkzeug für den Inferenzschluss von einer, in einer Stichprobe, ermittelten Häufigkeit auf die Häufigkeit in der Grundgesamtheit dar.
Dafür werden kritische Werte in Abhängigkeit der Stichprobengröße und der Häufigkeit, über die eine Aussage gemacht wird, bestimmt.
Bestimmung der kritischen Werte
Linksseitig getestete Hypothese:
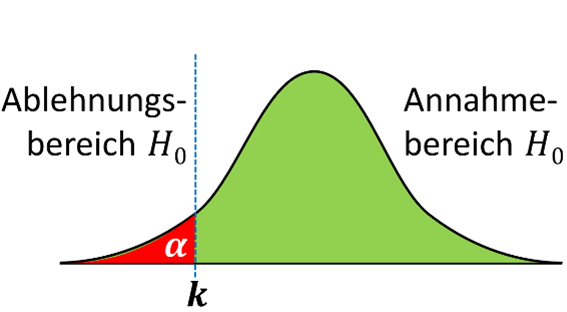
k=N\cdot p_{0}- z_{1-\alpha}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}Rechtsseitig getestete Hypothese:
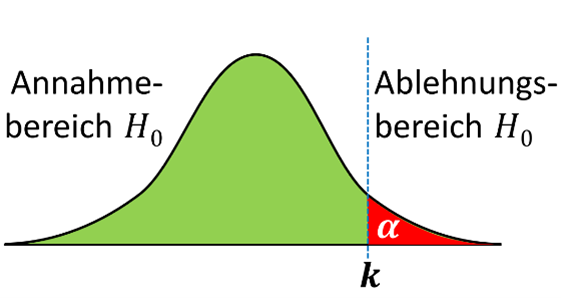
k=N\cdot p_{0}+ z_{1-\alpha}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}Zweiseitig getestete Hypothese:
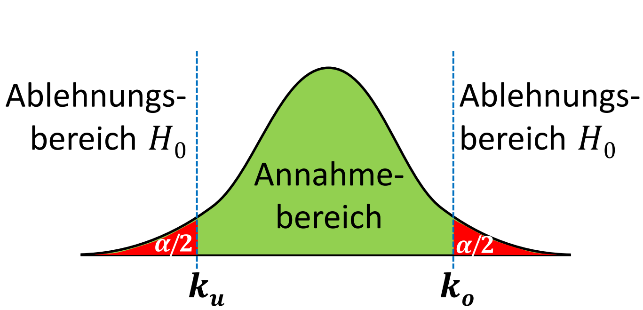
k_{u}=N\cdot p_{0}- z_{1-\frac{\alpha}{2}}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}k_{o}=N\cdot p_{0}+ z_{1-\frac{\alpha}{2}}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}Verwendete Kürzel
- „k“ ist der kritische Wert, ku ist der untere kritische Wert, ko ist der obere kritische Wert bei einem zweiseitigen Test.
- „N“ ist die Stichprobengröße.
- „p0“ ist die Häufigkeit, über die eine Aussage gemacht wird.
- „z“ ist der z-Wert.
- „α“ ist das Signifikanzniveau und steht für die Wahrscheinlichkeit der Menge von Testergebnissen, für die wir bereit sind, H0 zurückzuweisen, obwohl sie zutreffend ist. Meist werden das 5%- und das 1%-Signifikanzniveau verwendet (𝛼 = 0,05 bzw. 𝛼 = 0,01).
Häufige z-Werte sind folglich:
- 𝛼 = 0,05 und einseitig getestet: 1,64
- 𝛼 = 0,05 und zweiseitig getestet: 1,96
- 𝛼 = 0,01 und einseitig getestet: 2,33
- 𝛼 = 0,01 und zweiseitig getestet: 2,58
Voraussetzungen
Es muss gelten:
N\cdot p_{0}\cdot\left(1-p_{0}\right)>9Beispiele
Der linksseitige z-Test
Die ARD behauptet, dass mindestens 50 Prozent der Deutschen den „Tatort“ mögen. Medienforscherin Tina Franz bezweifelt das und sagt, es sind weniger.
Tina befragt 100 zufällig ausgewählte Deutsche, von denen 40 sagen, dass sie keinen Tatort mögen. Tina testet bei einem Signifikanzniveau von 5%.
H_{0}:p\geq0,5H_{1}:p<0,5k=N\cdot p_{0}- z_{1-\alpha}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}k=100\cdot 0,5- 1,64\cdot \sqrt{100\cdot 0,5\cdot \left(1-0,5\right)}k=50-8,2=41,8
Annahmebereich: [42; 100]
Ablehnungsbereich: [0; 41]
Die Nullhypothese muss abgelehnt werden, die Häufigkeit, die Tina ermittelt weicht signifikant vom Wert, den die ARD behauptet ab. Weniger als die Hälfte der Deutschen mögen den „Tatort“ (N=100, p < ,050).
Der rechtsseitig z-Test
Der Löwen-Sportvorstand behauptet, nicht mehr als 70 Prozent der Münchner:innen sind Bayern-Fans. Der FC-Bayern Chef sagt, es sind mehr.
Der FC-Bayern Chef gibt deshalb eine Studie in Auftrag, es werden 50 zufällig ausgewählte Münchner:innen befragt, von denen 42 sagen sie seien Bayern-Fans. In der Studie wird mit einem Signifikanzniveau von 5% getestet.
H_{0}:p\leq0,7H_{1}:p>0,7k=N\cdot p_{0}+ z_{1-\alpha}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}k=50\cdot 0,7+ 1,64\cdot \sqrt{50\cdot 0,7\cdot \left(1-0,7\right)}k=35+5,31=40,3
Annahmebereich: [0; 40]
Ablehnungsbereich: [41; 50]
Die Nullhypothese muss abgelehnt werden, die Häufigkeit, die in der Studie ermittelt wird, weicht signifikant vom Wert, den der Löwen-Sportvorstand behauptet ab. Mehr als 70% der Münchner:innen sind Bayern-Fans (N=50, p < ,050).
Der zweiseitige z-Test
Anna-Maria spielt „Mensch ärgere Dich nicht“ und vermutet, dass sie es mit einem gezinkten Würfel zu tun hat. Also würfelt sie 100-mal, dabei zeigt sich, dass die „1“ nur 12-mal vorkommt. Sie möchte bei einem Signifikanzniveau von 5% testen.
H_{0}:p=\frac{1}{6}H_{1}:p\neq\frac{1}{6}k_{u}=N\cdot p_{0}- z_{1-\frac{\alpha}{2}}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}k_{u}=100\cdot \frac{1}{6}- 1,96\cdot \sqrt{100\cdot \frac{1}{6}\cdot \left(1-\frac{1}{6}\right)}=9,4k_{o}=N\cdot p_{0}+ z_{1-\frac{\alpha}{2}}\cdot \sqrt{N\cdot p_{0}\cdot \left(1-p_{0}\right)}k_{o}=100\cdot \frac{1}{6}+ 1,96\cdot \sqrt{100\cdot \frac{1}{6}\cdot \left(1-\frac{1}{6}\right)}=24,0Annahmebereich: [10; 24]
Ablehnungsbereich: [0; 9] und [25; 100]
Die Nullhypothese darf angenommen werden, die Häufigkeit, die in der Studie ermittelt wird, weicht nicht signifikant vom erwarteten Wert für einen Würfel ab (N=100, p > ,050). Der Würfel ist mit hinreichender Sicherheit nicht gezinkt.
