t-Test für abhängige Stichproben

Der t-Test für abhängige Stichproben prüft, ob sich die Mittelwerte x̄₁ und x̄₂ in einer miteinander verbundenen Stichprobe systematisch voneinander unterscheiden. Statistisch prüft er, ob die zwei Stichproben aus einer Grundgesamtheit stammen, deren Parameter μ₁ und μ₂ identisch sind. Der t-Test für abhängige Stichproben wird bei gepaarten Beobachtungen sowie Messwiederholungen verwendet. Er wird auch als paired t-Test, t-Differenzentest, Differenzen-t-Test oder Paardifferenzentest bezeichnet.

Voraussetzungen des t-Tests für abhängige Stichproben

• Die Daten der Stichprobe entstammen einer normalverteilten Grundgesamtheit. Dafür ist nach dem zentralen Grenzwertsatz ein Stichprobenumfang größer 30 hinreichend.
• Die Differenzen der Wertepaare müssen normalverteilt sein. Dafür ist nach dem zentralen Grenzwertsatz ein Stichprobenumfang größer 30 hinreichend.
• Beide Stichproben müssen abhängigen Grundgesamtheiten entstammen.
• Die abhängige Variable ist dabei (quasi-)metrisch skaliert.

Signifikanztest des t-Tests für abhängige Stichproben

Um zu prüfen, ob sich die Mittelwerte mit hinreichender Sicherheit voneinander unterscheiden, wird der Signifikanztest des t-Tests für abhängige Stichproben gerechnet.

Einseitiges Problem:

H_{0}:\mu_{1}\leq \mu_{2}\qquad oder \qquad \mu_{1}\geq \mu_{2}\ 

H_{1}: \mu_{1}> \mu_{2}\qquad oder \qquad \mu_{1}< \mu_{2}\ 

Zweiseitiges Problem:

H_{0}: \mu_{1}=\mu_{2}

H_{1}: \mu_{1}\neq\mu_{2}

Signifikanztest:

Für den t-Test für abhängige Stichproben sind die Differenzen der Messwerte zentral:

d_{i}=x_{i1}-x_{i2}

So ist die Differenz der Mittelwerte der zentrale Stichprobenkennwert:

\bar{x}_{d}=\frac{\sum_{i=1}^Nd_{i}}{N}=\bar{x}_{1}-\bar{x}_{2}

Die Streuung des Stichprobenkennwerts ist:

s_{d}=\sqrt{\frac{{\sum_{i=1}^N({d_{i}-\bar{x}_{d})^2}}}{N-1}}

Der kritische t-Wert t_krit ist dann:

t=\sqrt{N}\cdot \frac{\bar{x}_{d}}{s_{d}} \qquad mit \qquad df=N-1

Testentscheidung nach festgelegtem Signifikanzniveau:

• Der kritische Wert t_krit kann unter Berücksichtigung des Signifikanzniveaus 𝛼 und der Freiheitsgrade df aus der t-Verteilungstabelle abgelesen werden.
• Wird einseitig getestet, entspricht der kritische Wert dem (1-α)-Quantil der t-Verteilung. Wird zweiseitig getestet, entspricht der kritische Wert dem (1-α/2)-Quantil der t-Verteilung. Der zweiseitige Test ist also konservativer.
• H₀ wird abgelehnt, wenn | t | > t_krit.

Effektstärke

Die Effektstärke gibt an, wie stark der Effekt der Gruppenzugehörigkeit auf die abhängige Variable ist. Nur wenn die Mittelwertdifferenz signifikant ist, findet eine Berechnung der Effektstärke statt.

Effektstärke d_z

Als standardisiertes Maß wird die Effektstärke d_z genutzt:

d_{z}=\frac{|\bar{x}_{d}|}{s_{d}}

Interpretationskonvention

• Betrag von Effektstärke d_z < 0,2: „kein Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Effektstärke d_z ≥ 0,2: „geringer Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Effektstärke d_z ≥ 0,5: „mittlerer Effekt der unabhängigen Variable auf die abhängige Variable“
• Betrag von Effektstärke d_z ≥ 0,8: „starker Effekt der unabhängigen Variable auf die abhängige Variable“

Das partielle Eta-Quadrat η_p²

Das partielle Eta-Quadrat η_p² ist das geläufige Maß, um die Effektstärke anzugeben. η_p²gibt an, welcher Anteil der Varianz der abhängigen Variable auf die Varianz der Gruppenzugehörigkeit zurückgeführt werden kann. Dafür wird zuerst der Populationseffekt geschätzt:

f_s^2=\frac{t^2}{df}

Damit lässt sich das partielle Eta-Quadrat errechnen:

\eta_p^2=\frac{f_s^2}{1+f_s^2}

Das partielle Eta-Quadrat wird im Forschungsbericht in Prozent angegeben.

Verwendete Kürzel

• N : Stichprobenumfang
• x_i1 (x_i2) : Wert eines Messwerts i der Gruppe 1 (2)
• x̄₁ (x̄₂) : Mittelwert in der Gruppe 1 (2)
• s_d : Streuung des Stichprobenkennwerts
• d_i : Differenz zweier Messwerte i
• x̄_d : Differenz der Mittelwerte
• d_z : Effektstärke d_z
• f_s² : Schätzung des Populationseffekts
• η_p² : partielles Eta-Quadrat

t-Test für abhängige Stichproben in R

Die Funktion t_test() aus dem tidycomm-Package berechnet unter anderem t-Tests für abhängige Stichproben. Die t_test()-Funktion gibt getrennt nach den zwei Gruppen in einer Tabelle die Stichprobenmittelwerte und Standartabweichungen an. Es wird der Name der abhängigen Variable, die Mittelwertdifferenz, der kritische t-Wert t_krit, die jeweiligen Freiheitsgrade und der p-Wert ausgegeben. Zusätzlich wird die Effektstärke d_z berechnet.

Für einen modifizierten incvlcomments-Datensatz lässt sich so ermitteln, ob Teilnehmende – themenunabhängig – Kommentare, die offensichtliche Drohungen enthalten, im Vergleich zu Kommentaren, die nur Beleidigungen/Profanitäten enthalten, als offensiver wahrnehmen.

Der modifizierte incvlcommnts-Datensatz enthält Bewertungen von zwei Kommentaren, die entweder bedrohlich („Threats“) oder beleidigend („Profanity“) verfasst sind. Dabei werden dieselben Probanden gebeten, beide Arten von Kommentaren zu bewerten, was bedeutet, dass jede Person zwei Ratings abgibt: einmal für „Threats“ und einmal für „Profanity“.

Hintergrund: Für den incvlcomments-Datensatz wurde ein Umfrageexperiment mit einer national repräsentativen Stichprobe von 964 deutschen Online-Nutzer:innen durchgeführt. Den Teilnehmenden wurden manipulierte Nutzerkommentare vorgelegt, die Aussagen enthielten, die mit einem unhöflichen Diskurs (z. B. Beleidigungen und Angriffe auf Argumente) und einem intoleranten Diskurs (z. B. beleidigende Stereotypen und Gewaltandrohungen) verbunden waren. Die Teilnehmer bewerteten die Kommentare, z. B. Beleidigung, Schaden für die Gesellschaft und ihre Absicht, den Kommentar, der die Aussage enthielt, zu löschen.

Für das Beispiel wird der Datensatz folgendermaßen modifiziert:

Befehl:

# Load your data
incvlcomments <- tidycomm::incvlcomments

# Add a new column to your data to indicate the type of comment
incvlcomments <- incvlcomments %>%
  mutate(type = case_when(
    profanity == 1 & violent_threats == 0 ~ "Profanity",
    profanity == 0 & violent_threats == 1 ~ "Threats",
    TRUE ~ NA_character_
  ))

# Remove all rows with NA in the new "type" column
incvlcomments <- incvlcomments %>%
  filter(!is.na(type))

# Remove all participants with more or less than two comment ratings
count_per_participant <- incvlcomments %>%
  group_by(participant_num) %>%
  summarize(count = n())

participants_to_remove <- count_per_participant %>%
  filter(count != 2) %>%
  pull(participant_num)

incvlcomments_filtered <- incvlcomments %>%
  filter(!(participant_num %in% participants_to_remove))

incvlcomments_filtered %>%
  dplyr::group_by(type) %>%
  describe(offensiveness)

Zunächst wird mit der describe()-Funktion aus dem tidycomm-Package und der group_by-Funktion aus dem dplyr-Package ermittelt, ob alle Voraussetzungen erfüllt sind.

Befehl:

incvlcomments_filtered %>%
  dplyr::group_by(type) %>%
  describe(offensiveness)

Ausgabe:

# A tibble: 2 × 16
# Groups:   type [2]
  type      Variable          N Missing     M    SD   Min   Q25   Mdn   Q75   Max Range CI_95_LL CI_95_UL Skewness Kurtosis
* <chr>     <chr>         <int>   <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>    <dbl>    <dbl>
1 Profanity offensiveness   480       0  3.91  2.02     1  2      4    5.67     7     6     3.72     4.09   0.0490     1.76
2 Threats   offensiveness   480       0  5.07  1.94     1  3.67   5.5  7        7     6     4.89     5.24  -0.702      2.31

Nachdem die Stichprobe größer 30 ist, darf nach dem zentralen Grenzwertsatz eine Normalverteilung der Grundgesamtheit angenommen werden. Beide Stichproben entstammen abhängigen Grundgesamtheiten. Nachdem die verbundene Stichprobe größer 30 ist, darf nach dem zentralen Grenzwertsatz eine Normalverteilung der Differenzen der Wertepaare angenommen werden. Die abhängige Variable, wie beleidigend und feindselig der Kommentar wahrgenommen wird, (offensiveness) ist quasimetrisch angegeben („Bewerten Sie die Aussage, ob der Kommentar als beleidigend und feindselig empfunden wird (Skala von 1 bis 7)“), die Gruppierungsvariable (type) ist dichotom (Profanity oder Threats). Somit darf der t-Test für abhängige Stichproben gerechnet werden.

Befehl:

incvlcomments_filtered %>% t_test(type, offensiveness, paired = TRUE, case_var = participant_num)

Ausgabe:

# A tibble: 1 × 12
  Variable      M_Threats SD_Threats M_Profanity SD_Profanity   Delta_M         t    df         p         d Levene_p var_equal
* <chr>         <num:.3!>  <num:.3!>   <num:.3!>    <num:.3!> <num:.3!> <num:.3!> <dbl> <num:.3!> <num:.3!>    <dbl> <chr>    
1 offensiveness     5.067      1.936       3.906        2.022     1.162    10.463   479     0.000     0.587     0.13 TRUE 

Es ist auch möglich mehrere abhängige Variablen zu testen. Dafür werden diese Variablen ergänzt. Oder es wird keine abhängige Variable angegeben, dann testet die t_test()-Funktion alle metrischen Variablen im Datensatz (vgl. t-Test für unabhängige Stichproben).

Visualisieren von t-Tests für abhängige Stichproben

Eine Visualisierung ist über die Funktion visualize() möglich:

Befehl:

incvlcomments_filtered %>% t_test(type, offensiveness, paired = TRUE, case_var = participant_num) %>%
  visualize()

Ausgabe:

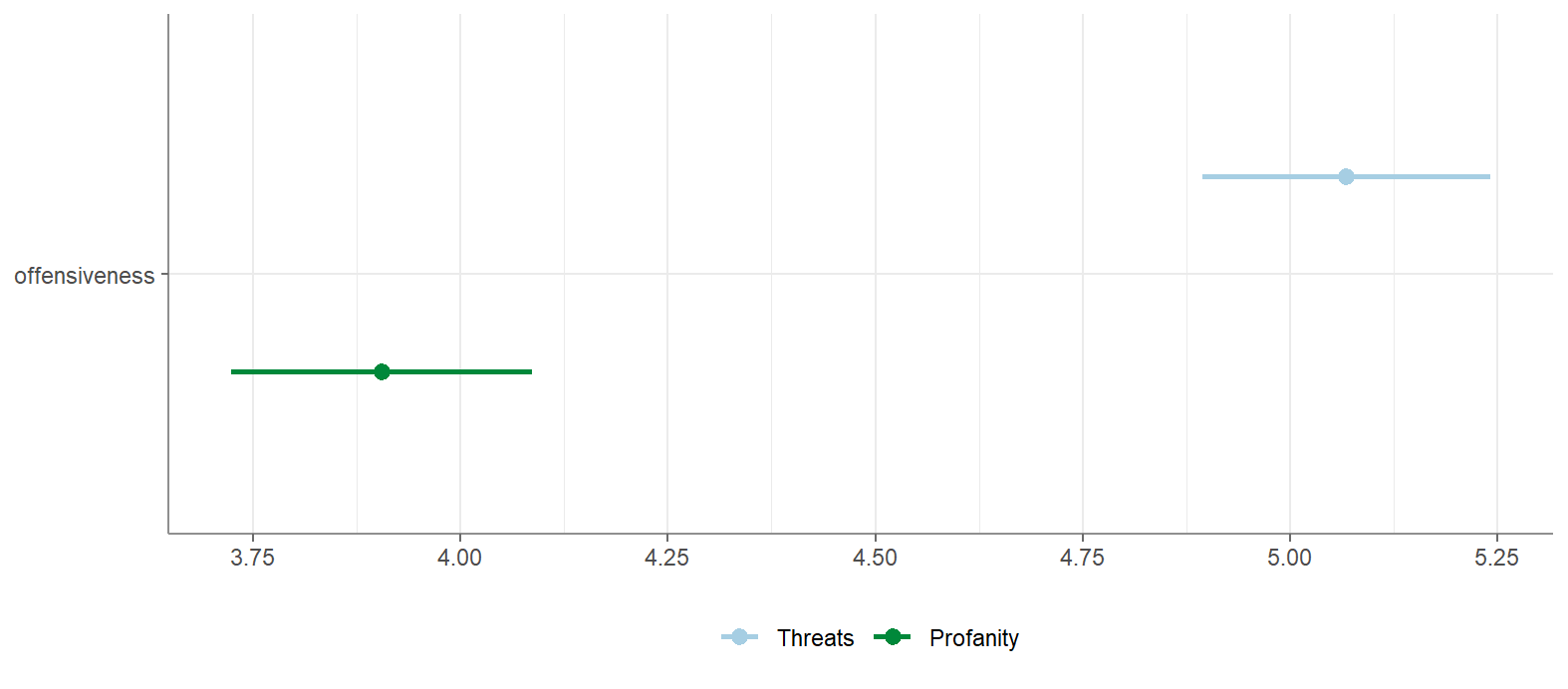
t-Tests für abhängige Stichproben berichten

Notwendige Informationen

• Stichprobenumfang N
• Mittelwerte der Gruppen 1 (2): M₁ (M₂)
• Standardabweichungen der Gruppen 1 (2): SD₁ (SD₂)
• Kritischer t-Wert t_krit mit den Freiheitsgraden df
• Signifikanz und jeweiliges Signifikanzniveau des Zusammenhangs
• Effektstärke d_z
• Partielles Eta-Quadrat η_p²

Beispielbericht

„Die Hypothese konnte bestätigt werden. Teilnehmende nehmen Kommentare, die offensichtliche Drohungen enthalten, als signifikant offensiver wahr im Vergleich zu Kommentaren, die nur Beleidigungen/Profanitäten enthalten, unabhängig vom spezifischen Thema des Kommentars. Der Effekt mittlerer Stärke erklärt 18,6% der empirischen Varianz (N = 480; M_Threats = 5,07 ; SD_Threats = 1,94; M_Profanity = 3,91; SD_Profanity = 2,02; t(479) = 10,463; p < ,001; d_z = ,59; η_p² = .186).“